If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
GNSS Measurements Modelling: Difference between revisions
Jaume.Sanz (talk | contribs) No edit summary |
Jaume.Sanz (talk | contribs) No edit summary |
||
| Line 24: | Line 24: | ||
<math>\Phi_{_1}=\rho+c(\delta t_{rcv}-\delta t^{sat})+Tr- \tilde{\alpha_1}(I+K_{21})+b_1+\lambda_1\,N_1+\lambda_1 w+m_1+\epsilon_1 \qquad \mbox{(1)}</math> | <math>\Phi_{_1}=\rho+c(\delta t_{rcv}-\delta t^{sat})+Tr- \tilde{\alpha_1}(I+K_{21})+b_1+\lambda_1\,N_1+\lambda_1 w+m_1+\epsilon_1 \qquad \mbox{(1)}</math> | ||
where the satellite clock offset <math>\delta t^{sat}</math> includes the [[Relativistic Clock | where the satellite clock offset <math>\delta t^{sat}</math> includes the [[Relativistic Clock Correction|relativistic clock correction]] and range <math>\rho</math> the [[Relativistic Path Range Effect|relativistic path correction]]. | ||
The residuals between the measured and predicted code or carrier pseudoranges,contain the receiver position error and clock offsets, plus miss-modelling and measurement noise errors. These residuals, that from hereafter will be called prefit-residuals, are the input data for the [[Solving Navigation Equations|navigation equations]]. Such equations consist on a linear system which solution by Least Squares of the [[Kalman Filter|Kalman filtering]] allows to decorrelate (i.e., separate) the different error components from the prefit residuals and, thence, to determine the receiver coordinates. The more accurate measurement modelling is performed, the better decorrelation of errors is achieved and, thence, more accurate coordinates are obtained. | The residuals between the measured and predicted code or carrier pseudoranges,contain the receiver position error and clock offsets, plus miss-modelling and measurement noise errors. These residuals, that from hereafter will be called prefit-residuals, are the input data for the [[Solving Navigation Equations|navigation equations]]. Such equations consist on a linear system which solution by Least Squares of the [[Kalman Filter|Kalman filtering]] allows to decorrelate (i.e., separate) the different error components from the prefit residuals and, thence, to determine the receiver coordinates. The more accurate measurement modelling is performed, the better decorrelation of errors is achieved and, thence, more accurate coordinates are obtained. | ||
Revision as of 10:51, 27 January 2012
| Fundamentals | |
|---|---|
| Title | GNSS Measurements Modelling |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Basic |
| Year of Publication | 2011 |
The aim of this article is to provide the background for the measurement's modelling for the Standard and Precise Point Positioning. Applying this modelling, the user-receiver would correct each measurement from the known delay.
Introduction
The code and carrier phase measurements contains several additional time delays associated to the signal propagation or to the clocks, among the geometric range between the satellite and receiver (see GNSS basic observables). These delays are common for code and carrier measurements, except for the wind-up and the ambiguities that affect only to the carrier measurements, and for a sign in the ionospheric refraction, delaying the code and advancing the carrier measurements (see Ionospheric Delay).
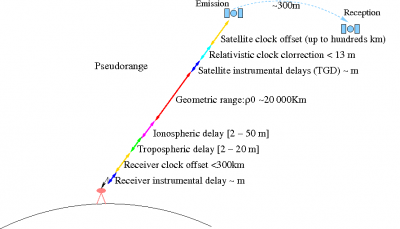
Figure 1 shows a layout of the diferent time-delays terms in the pseudorange to illustrate the measurements content.
Regarding the combination of pairs of signals, the measurements can be modelled by the following equations:
[math]\displaystyle{ R_{_1}=\rho+c(\delta t_{rcv}-\delta t^{sat})+Tr+\tilde{\alpha_1}(I+K_{21})+\mathcal{M}_1+\varepsilon_1 }[/math]
[math]\displaystyle{ \Phi_{_1}=\rho+c(\delta t_{rcv}-\delta t^{sat})+Tr- \tilde{\alpha_1}(I+K_{21})+b_1+\lambda_1\,N_1+\lambda_1 w+m_1+\epsilon_1 \qquad \mbox{(1)} }[/math]
where the satellite clock offset [math]\displaystyle{ \delta t^{sat} }[/math] includes the relativistic clock correction and range [math]\displaystyle{ \rho }[/math] the relativistic path correction.
The residuals between the measured and predicted code or carrier pseudoranges,contain the receiver position error and clock offsets, plus miss-modelling and measurement noise errors. These residuals, that from hereafter will be called prefit-residuals, are the input data for the navigation equations. Such equations consist on a linear system which solution by Least Squares of the Kalman filtering allows to decorrelate (i.e., separate) the different error components from the prefit residuals and, thence, to determine the receiver coordinates. The more accurate measurement modelling is performed, the better decorrelation of errors is achieved and, thence, more accurate coordinates are obtained.
Related Articles
In the following entries, the GNSS measurements modelling is split into their different contributors: