If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Sidereal Time: Difference between revisions
Jump to navigation
Jump to search
Jaume.Sanz (talk | contribs) No edit summary |
Jaume.Sanz (talk | contribs) No edit summary |
||
| Line 7: | Line 7: | ||
|Title={{PAGENAME}} | |Title={{PAGENAME}} | ||
}} | }} | ||
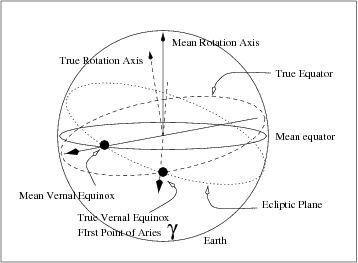
The reference is the Vernal Equinox, or the Aries point, which is defined as the intersection between the equator and the ecliptic plane <ref group="footnotes"> Ecliptic: Apparent circular path of the sun on the celestial sphere during the course of a year. The plane of the ecliptic is inclined an angle of about 23<math>^{o}</math>26<math>^' | The reference is the Vernal Equinox, or the Aries point, which is defined as the intersection between the equator and the ecliptic plane <ref group="footnotes"> Ecliptic: Apparent circular path of the sun on the celestial sphere during the course of a year. The plane of the ecliptic is inclined an angle of about 23<math>^{o}</math>26<math>^'</math> with respect to the celestial equator, see equation (5) in [[ICRF to CEP]].</ref>. Two types of Aries point can be considered depending on which equator plane is considered (i.e, the mean equator or the true equator). | ||
Revision as of 08:41, 19 January 2012
| Fundamentals | |
|---|---|
| Title | Sidereal Time |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Basic |
| Year of Publication | 2011 |
The reference is the Vernal Equinox, or the Aries point, which is defined as the intersection between the equator and the ecliptic plane [footnotes 1]. Two types of Aries point can be considered depending on which equator plane is considered (i.e, the mean equator or the true equator).
- Mean Aries point: Is the intersection of mean equator (the effect of Precession over the earth rotation axis is taken into account, see article Transformation between Celestial and Terrestrial Frames) with ecliptic [footnotes 2], see figure 1.
- True Aries point: Defined as the intersection between the true equator [footnotes 3] (the effects of Precession and Nutation of earth rotation pole have been taken into account, see article Transformation between Celestial and Terrestrial Frames) with the Ecliptic [footnotes 4], see figure 1.
According to the previous definitions, four classes of sidereal times are introduced:
- Local "Apparent" Sidereal Time (LAST)([math]\displaystyle{ \Theta }[/math]): is the hour angle of the "true" Aries point (from local meridian) [footnotes 5].
- Greenwich "Apparent" Sidereal Time (GAST)([math]\displaystyle{ \Theta_{_G} }[/math]): is the hour angle of "true" Aries point, from Greenwich meridian.
- Local Mean Sidereal Time (LMST)([math]\displaystyle{ \theta }[/math]): the same that LAST with the mean equinox.
- Greenwich Mean Sidereal Time (GMST)([math]\displaystyle{ \theta_{_G} }[/math]): the same that GAST with the mean equinox.
The Figure 2 summaries these four sidereal times.
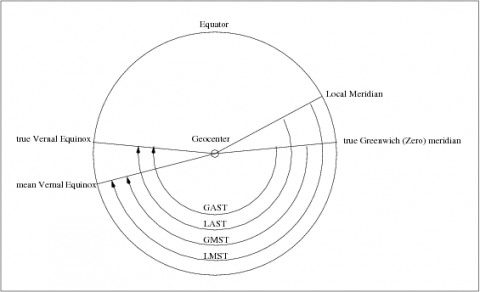Figure 2: Different sidereal Times (from > [Seeber, 1993] [1]
Notes
- ^ Ecliptic: Apparent circular path of the sun on the celestial sphere during the course of a year. The plane of the ecliptic is inclined an angle of about 23[math]\displaystyle{ ^{o} }[/math]26[math]\displaystyle{ ^' }[/math] with respect to the celestial equator, see equation (5) in ICRF to CEP.
- ^ Actually, the mean ecliptic. Like earth rotation pole, Ecliptic pole suffers a Precession and Nutation effect due to the perturbation of moon and major planets on earth orbit. Nevertheless its amplitude is 50 times shorter than the earth rotation pole and, at the level of accuracy required here, we will not distinguish between mean or true ecliptic.
- ^ This equator is defined as the plane that contains the Geocenter and is orthogonal to the instantaneous daily rotation axis.
- ^ Due to the accuracies needed, it is enough to compute the true Aries point using mean Ecliptic plane. We will refer to this plane always as "the ecliptic", without distinguishing between the mean or the true one.
- ^ Apparent in Astronomy refers to what is seen from an Ideal earth's centre, without atmosphere and rotation. With these conditions the effects of light refraction, light aberration and parallax has been suppressed.
References
- ^ [Seeber, 1993] Seeber, G., 1993. Satellite Geodesy: Foundations, Methods, and Applications. Walter de Gruyter & Co., Berlin, Germany.