If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Transformations between ECEF and ENU coordinates
| Fundamentals | |
|---|---|
| Title | Transformations between ECEF and ENU coordinates |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Advanced |
| Year of Publication | 2011 |
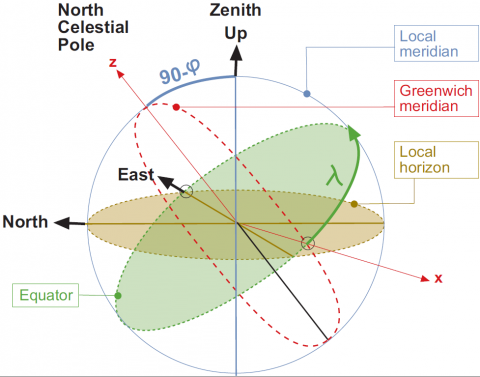
The relation between the local East, North, Up (ENU) coordinates and the [math]\displaystyle{ (x,y,z) }[/math] Earth Centred Earth Fixed (ECEF) coordinates is illustrated in the next figure:
From the figure 1 it follows that the ENU coordinates can be transformed to the [math]\displaystyle{ (x,y,z) }[/math] ECEF by two rotations, where [math]\displaystyle{ \varphi }[/math] and [math]\displaystyle{ \lambda }[/math] are, respectively, the latitude and longitude from the ellipsoid:
- 1. A clockwise rotation over east-axis by an angle [math]\displaystyle{ 90-\varphi }[/math] to align the up-axis with the [math]\displaystyle{ z }[/math]-axis. That is [math]\displaystyle{ {\mathbf R}_1[-(\pi/2-\varphi)] }[/math].
- 2. A clockwise rotation over the [math]\displaystyle{ z }[/math]-axis by an angle [math]\displaystyle{ 90+\lambda }[/math] to align the east-axis with the [math]\displaystyle{ x }[/math]-axis. That is [math]\displaystyle{ {\mathbf R}_3[-(\pi/2+\lambda)] }[/math].
That is:
- [math]\displaystyle{ \left [ \begin{array}{l} x\\ y\\ z\\ \end{array} \right ] = {\mathbf R}_3[-(\pi/2+\lambda)]\,{\mathbf R}_1[-(\pi/2-\varphi)] \left [ \begin{array}{l} E\\ N\\ U\\ \end{array} \right ] \qquad \mbox{(1)} }[/math]
where, according to the expressions (2) (see Transformation between Terrestrial Frames)
- [math]\displaystyle{ \begin{array}{l} \mathbb{\mathbf R}_1[\theta]=\left [ \begin{array}{ccc} 1 & 0 & 0\\ 0 & \cos \theta & \sin \theta \\ 0 & -\sin \theta & \cos \theta \\ \end{array} \right ] \;;\;\; \mathbb{\mathbf R}_2[\theta]=\left [ \begin{array}{ccc} \cos \theta & 0 & -\sin \theta \\ 0 & 1 & 0\\ \sin \theta &0 & \cos \theta \\ \end{array} \right ]\\ \\ \mathbb{\mathbf R}_3[\theta]=\left [ \begin{array}{ccc} \cos \theta & \sin \theta &0\\ -\sin \theta & \cos \theta & 0\\ 0 & 0 & 1\\ \end{array} \right ] \end{array} \qquad \mbox{(2)} }[/math]
yields:
- [math]\displaystyle{ {\mathbf R}_3[-(\pi/2+\lambda)]\,{\mathbf R}_1[-(\pi/2-\varphi)]= \left ( \begin{array}{ccc} -\sin \lambda & -\cos \lambda \sin \varphi &\cos \lambda \cos \varphi\\ \cos \lambda & -\sin \lambda \sin \varphi & \sin \lambda \cos \varphi\\ 0 & \cos \varphi & \sin \varphi\\ \end{array} \right ) \qquad \mbox{(3)} }[/math]
The unit vectors in local East, North and Up directions as expressed in ECEF cartesian coordinates are given by the columns of matrix (3). That is:
- [math]\displaystyle{ \begin{array}{l} \hat{\mathbf e}=\left ( -\sin \lambda \,,\,\cos \lambda\,,\, 0 \right )\\ \hat{\mathbf n}=\left ( - \cos \lambda \sin \varphi \,,\,- \sin \lambda \sin \varphi\,,\, \cos \varphi \right)\\ \hat{\mathbf u}=\left ( \cos \lambda \cos \varphi \,,\,\sin \lambda\ \cos \varphi\,,\, \sin \varphi \right) \qquad \mbox{(4)} \end{array} }[/math]
Note: If [math]\displaystyle{ (\lambda,\varphi) }[/math] are ellipsoidal coordinates, thence, the vector [math]\displaystyle{ \hat{\mathbf u} }[/math] is orthogonal to the tangent plane to the ellipsoid, which is defined by [math]\displaystyle{ (\hat{\mathbf e}, \hat{\mathbf n}) }[/math]. If [math]\displaystyle{ (\lambda,\varphi) }[/math] are taken as the spherical longitude and latitude, thence, the vector [math]\displaystyle{ \hat{\mathbf u} }[/math] is in the radial direction and [math]\displaystyle{ (\hat{\mathbf e}, \hat{\mathbf n}) }[/math] defines the tangent plane to the sphere.
From ECEF to ENU coordinates
Taking into account the properties of the rotation matrices [math]\displaystyle{ {\mathbf R}_i(\alpha) }[/math],i.e., [math]\displaystyle{ {\mathbf R}_i^{-1}(\alpha)= {\mathbf R}_i(-\alpha)={\mathbf R}_i^T(\alpha) }[/math], thence, the inverse transformation of (1) is given by:
- [math]\displaystyle{ \left [ \begin{array}{l} E\\ N\\ U\\ \end{array} \right ] = {\mathbf R}_1[\pi/2-\varphi]\,{\mathbf R}_3[\pi/2+\lambda] \left [ \begin{array}{l} x\\ y\\ z\\ \end{array} \right ] \qquad \mbox{(5)} }[/math]
where the transformation matrix of (5) is the transpose of matrix (3):
- [math]\displaystyle{ {\mathbf R}_1[\pi/2-\varphi]\,{\mathbf R}_3[\pi/2+\lambda]= \left ( \begin{array}{ccc} -\sin \lambda & \cos \lambda &0\\ - \cos \lambda \sin \varphi & -\sin \lambda \sin \varphi & \cos \varphi\\ \cos \lambda \cos \varphi & \sin \lambda \cos \varphi & \sin \varphi\\ \end{array} \right ) \qquad \mbox{(6)} }[/math]
The unit vectors in the ECEF [math]\displaystyle{ \hat{\mathbf x} }[/math], [math]\displaystyle{ \hat{\mathbf y} }[/math] and [math]\displaystyle{ \hat{\mathbf z} }[/math] directions, as expressed in ENU coordinates, are given by the columns of matrix (6). That is:
- [math]\displaystyle{ \begin{array}{l} \hat{\mathbf x}=\left ( -\sin \lambda \,,\,-\cos \lambda \sin \varphi\,,\, \cos \lambda \cos \varphi \right )\\ \hat{\mathbf y}=\left (\cos \lambda\,,\,- \sin \lambda \sin \varphi\,,\, \sin \lambda \cos \varphi \right)\\ \hat{\mathbf z}=\left ( 0 \,,\, \cos \varphi \,,\,\sin \varphi \right) \end{array} \qquad \mbox{(7)} }[/math]
Elevation and azimuth computation
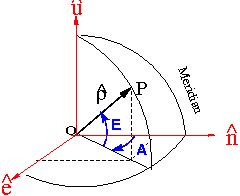
Given the line of sight unit vector
- [math]\displaystyle{ \hat {\boldsymbol \rho}=\displaystyle \frac{{\mathbf r}^{sat}-{\mathbf r}_{rcv}}{\| {\mathbf r}^{sat}-{\mathbf r}_{rcv} \|} \qquad \mbox{(8)} }[/math]
where [math]\displaystyle{ {\mathbf r}^{sat} }[/math] and [math]\displaystyle{ {\mathbf r}_{rcv} }[/math] are the geocentric position of the satellite and receiver, respectively, the elevation and azimuth in the local system coordinates (ENU), defined by the unit vectors [math]\displaystyle{ \hat{\mathbf e} }[/math], [math]\displaystyle{ \hat{\mathbf n} }[/math] and [math]\displaystyle{ \hat{\mathbf u} }[/math] can be computed from (see figure 2):
- [math]\displaystyle{ \begin{array}{l} \hat {\boldsymbol \rho}\cdot \hat{\mathbf e} =\cos E \sin A\\ \hat {\boldsymbol \rho}\cdot \hat{\mathbf n}=\cos E \cos A\\ \hat {\boldsymbol \rho}\cdot \hat{\mathbf u} = \sin E \end{array} \qquad \mbox{(9)} }[/math]
Thence the elevation and azimuth of satellite in the local coordinates system are given by:
- [math]\displaystyle{ E=\arcsin(\hat {\boldsymbol \rho}\cdot \hat{\mathbf u}) \qquad \mbox{(10)} }[/math]
- [math]\displaystyle{ A=\arctan \left (\frac{\hat {\boldsymbol \rho}\cdot \hat{\mathbf e}}{\hat {\boldsymbol \rho}\cdot \hat{\mathbf n}}\right ) \qquad \mbox{(11)} }[/math]
Note: If [math]\displaystyle{ (\lambda,\varphi) }[/math] are ellipsoidal coordinates, thence, the vector [math]\displaystyle{ \hat{\mathbf u} }[/math] is orthogonal to the tangent plane to the ellipsoid, which is defined by [math]\displaystyle{ (\hat{\mathbf e}, \hat{\mathbf n}) }[/math]. If [math]\displaystyle{ (\lambda,\varphi) }[/math] are taken as the spherical longitude and latitude, thence, the vector [math]\displaystyle{ \hat{\mathbf u} }[/math] is in the radial direction and [math]\displaystyle{ (\hat{\mathbf e}, \hat{\mathbf n}) }[/math] defines the tangent plane to the sphere.