If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Transformation between Celestial and Terrestrial Frames
| Fundamentals | |
|---|---|
| Title | Transformation between Celestial and Terrestrial Frames |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Intermediate |
| Year of Publication | 2011 |
Coordinate transformations between CRF and TRF frames are performed by mean of rotations corresponding to Precession, Nutation and Pole movement, briefly described as follows.
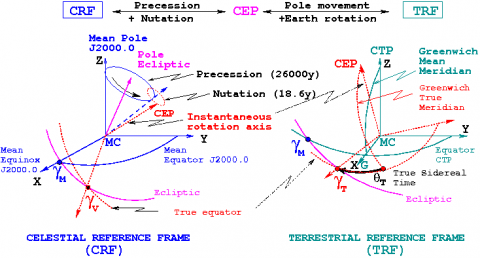
- Precession and nutation [forced rotation]: Earth rotation axis (and its equatorial plane) is not kept fixed in space, i.e., in relation to so called ”fixed-stars”, but it rotates about the pole of the ecliptic, as it is shown in figure 1. This movement is due to the effect of the gravitational attraction of the moon and the sun and major planets over the terrestrial ellipsoid. The total movement can be split into a secular component (precession, with a period of 26 000 years) and a periodic component (nutation, with a period of 18.6 years).
- Pole movement [free rotation]: Due to the structure of the earth's mass distribution and its variation, the earth’s rotation axis is not fixed in relation to the earth’s crust. It moves around on the surface of the earth within a square of about 20 meters in relation to a point with fixed coordinates on earth. This movement has a period of about 430 sidereal days (Chandler period). On the other hand, earth rotation velocity is not constant, but it changes in time (although in very small quantities[footnotes 1]), as it was mentioned in the previous section.
The detailed expressions for transformation between the CRF and TRF frames are provided in Transforming Celestial to Terrestrial Frames. The next equations briefly summarise such transformation:
For a given epoch t, the coordinates transformation can be decomposed in a rotation matrices (i.e., orthogonal matrices)[footnotes 2] product as:
- [math]\displaystyle{ [TRF] = R_M(t) R_S(t) N(t) P(t) [CRF] \qquad \mbox{(1)} }[/math]
being the inverse transformation:
- [math]\displaystyle{ [CRF] = P^T(t)N^T(t) R_S^T(t) R_M^T(t) [TRF] \qquad \mbox{(2)} }[/math]
where:
- - [CRF] Coordinates Vector in the Celestial Reference Frame.
- - [TRF] Coordinates Vector in the Terrestrial Reference Frame.
- - P Transformation matrix associated to the precession between the reference epoch and the epoch t.
- - N Transformation matrix associated to the nutation at epoch t.
- - RS Transformation matrix associated to the earth rotation around the Conventional Ephemeris Pole (CEP) axis.
- - RM Transformation matrix associated to the polar motion.
The matrices P and N are associated to the rotations needed to transform the coordinates from [CRF] to the [CEP]. They are provided by analytical expressions without requiring external parameters (see ICRF to CEP).
The matrices RS and RM are associated to the rotations needed to transform the coordinates from [CEP] to the [TRF]. Their computation requires the Earth Rotation Parameters (ERP) and Earth Orientation Parameters (EOP) files that are actualised periodically (see this website). More details can be found in CEP to ITRF.
The transformation matrix for the polar motion is (see equation (9) in CEP to ITRF):
- [math]\displaystyle{ R_M(t) = R_2(-x_p) R_1(-y_p) \qquad \mbox{(3)} }[/math]
where [math]\displaystyle{ x_p }[/math] and [math]\displaystyle{ y_p }[/math] are the coordinates of the CEP in the TRF, and [math]\displaystyle{ R_1 }[/math], [math]\displaystyle{ R_2 }[/math] are the rotation matrices defined by (4) (see Transformation between Terrestrial Frames)
[math]\displaystyle{ \begin{array}{l} \mathbb{\mathbf R}_1[\theta]=\left [ \begin{array}{ccc} 1 & 0 & 0\\ 0 & \cos \theta & \sin \theta \\ 0 & -\sin \theta & \cos \theta \\ \end{array} \right ] \;;\;\; \mathbb{\mathbf R}_2[\theta]=\left [ \begin{array}{ccc} \cos \theta & 0 & -\sin \theta \\ 0 & 1 & 0\\ \sin \theta &0 & \cos \theta \\ \end{array} \right ]\\ \\ \mathbb{\mathbf R}_3[\theta]=\left [ \begin{array}{ccc} \cos \theta & \sin \theta &0\\ -\sin \theta & \cos \theta & 0\\ 0 & 0 & 1\\ \end{array} \right ] \end{array} \qquad \mbox{(4)} }[/math]
The transformation matrix associated to the earth rotation around the CEP axis is given by (see equation (2) in CEP to ITRF):
- [math]\displaystyle{ R_S(t)= R_3(\Theta_{_G}) \qquad \mbox{(5)} }[/math]
where [math]\displaystyle{ \Theta_{_G} }[/math] is the Greenwich true sidereal time at epoch t and [math]\displaystyle{ R_3 }[/math] is from (4).
Figure 1 outlines the transformation between celestial (CRF) and terrestrial (TRF) frames: Through precession and nutation corrections, the Mean Equator and Equinox J2000.0 are transformed to True Equator and Equinox at observation epoch. They define a reference system with the Z-axis in the direction of the instantaneous rotation axis of earth (Conventional Ephemeris Pole, CEP), and X-axis pointing to true Aries point. Finally, using Earth Rotation Parameters (ERP) and Earth Orientation Parameters (EOP) (i.e., pole movement data), the CEP system is transformed to TRF[footnotes 3].
For more detailed information on this transformation, please refer to Transforming Celestial to Terrestrial Frames.
Notes
- ^ Due to friction of water in shallow seas, atmosphere movements, abrupt displacements in the earth interior (in 1955, the rotation suddenly delayed by 41s · 10−6), etc. Note that TRS system is tied to Greenwich meridian and therefore, it rotates with the earth.
- ^ Note: These matrices verify: [math]\displaystyle{ {R}^{T}(\theta)={R}^{-1}(\theta)={R(-\theta)} }[/math].
- ^ Precession and Nutation series (defined for the mean equator and equinox J2000.0 in CRF frame) have valid analytical expressions for long time intervals. But the rotation and orientation parameters of earth can not be modelled theoretically and must be periodically updated using observations.