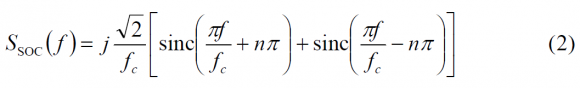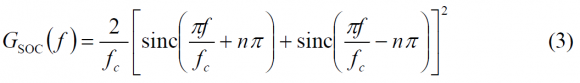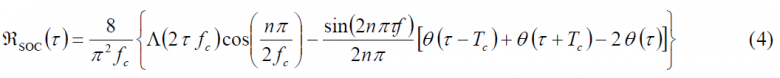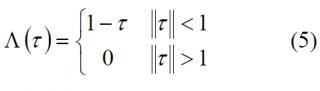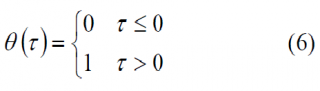If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Sinusoidal Binary Offset Carrier (SOC) Signals
| Fundamentals | |
|---|---|
| Title | Sinusoidal Binary Offset Carrier (SOC) Signals |
| Author(s) | J.A Ávila Rodríguez, University FAF Munich, Germany. |
| Level | Advanced |
| Year of Publication | 2011 |
To derive the spectrum of the SOC signals, the most convenient is to use the convolution theorem. According to it, the Fourier transform of the chip waveform can be expressed in terms of a convolution between the modulating carrier and the code bit. The problem reduces then to calculating the Fourier transforms for each signal as shown in [J. Winkel, 2002] [1]. In fact:
which can be further simplified as follows, assuming that the code is ideal:
Therefore, the power spectral density adopts the following form:
It is interesting to note also that the same distinction between even and odd SOCs can also be made here as with the rectangular signals that we have already studied. Furthermore, the maximum of the spectrum is not located at [math]\displaystyle{ f = n f_c }[/math] as one might expect, but somewhere close to that point as shown in [J. Winkel, 2002] [1]. Finally, the autocorrelation function of the SOC signal for the sine-phased case is shown to be [J. Winkel, 2002] [1]:
where [math]\displaystyle{ \Lambda \left ( \tau \right ) }[/math] is the triangular function and [math]\displaystyle{ \Theta \left ( \tau \right ) }[/math] represents the Heaviside step function. As we know the triangular function is defined as follows:
and the Heaviside step function is equally shown to be defined as:
References
Credits
The information presented in this NAVIPEDIA’s article is an extract of the PhD work performed by Dr. Jose Ángel Ávila Rodríguez in the FAF University of Munich as part of his Doctoral Thesis “On Generalized Signal Waveforms for Satellite Navigation” presented in June 2008, Munich (Germany)