If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Relativistic Clock Correction
| Fundamentals | |
|---|---|
| Title | Relativistic Clock Correction |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Intermediate |
| Year of Publication | 2011 |
The rate of advance of two identical clocks, placed one in the satellite and the other on the terrestrial surface, will differ due to the difference of the gravitational potential (general relativity) and to the relative speed between them (special relativity). This difference can be split into [1]:
- A constant component that only depends on the nominal value of the semi-major axis of the satellite orbit, which is adjusted modifying (in factory) the clock oscillating frequency of the satellite[footnotes 1]:
- [math]\displaystyle{ \frac{f_0'-f_0}{f_0}=\frac{1}{2} \left( \frac{v}{c} \right) ^2+\frac{\triangle U}{c^2} \simeq -4.464 \cdot 10^{-10} \qquad \mbox{(1)} }[/math]
- A periodical component due to the orbit eccentricity (that must be applied by the user receiver software):
- [math]\displaystyle{ \Delta_{rel}=- 2\, \frac{\mathbf{r}^{sat} \cdot \mathbf{v}^{sat}}{c^2} \qquad \mbox{(2)} }[/math]
- where [math]\displaystyle{ {\mathbf r}^{sat} }[/math] and [math]\displaystyle{ {\mathbf v}^{sat} }[/math] are the satellite position ([math]\displaystyle{ \displaystyle m }[/math]) and velocity ([math]\displaystyle{ \displaystyle m/s }[/math]) vectors, in an inertial system[footnotes 2]. The scalar [math]\displaystyle{ {\mathbf r}^{sat}\cdot{\mathbf v}^{sat} }[/math] can be evaluated either in a CRS or TRS (i.e., ECEF) system. Notice that in a ECEF system, the earth rotation [math]\displaystyle{ {\boldsymbol \omega}_E \times {\mathbf r}^{sat} }[/math] should be discounted from [math]\displaystyle{ {\mathbf v}^{sat} }[/math], but it cancels in the scalar product with [math]\displaystyle{ {\mathbf r}^{sat} }[/math].
Unlike in GPS, relativistic corrections to GLONASS orbits eccentricity are transmitted within the navigation message into the satellite clock corrections ([math]\displaystyle{ \displaystyle \tau_n }[/math], [math]\displaystyle{ \displaystyle \gamma_n }[/math]). Thence, (2) is not needed with such broadcast message [1].
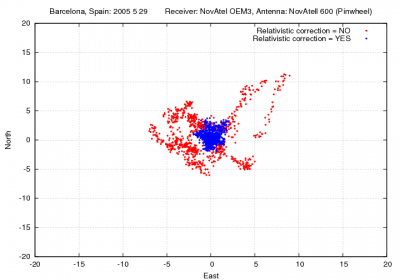
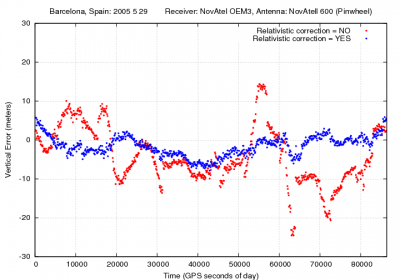
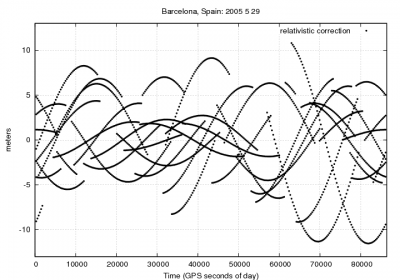
Figure 1 illustrates the effect of neglecting the relativistic correction given by equation (2) on the user position. As it is shown, range errors up to [math]\displaystyle{ 13 }[/math] meters and vertical errors over [math]\displaystyle{ 20 }[/math] meters can be experienced when neglecting this correction.
Figure 1: Relativistic correction: Range and position domain effect First row shows the horizontal (left) and vertical (right) positioning error using (blue) or not using (red) the relativistic correction 2. The variation in range, in meters units, is shown in the second row at left.
Notes
- ^ Being [math]\displaystyle{ \displaystyle f_0=10.23 MHz }[/math], one has [math]\displaystyle{ \Delta f_0= 4.464 \cdot 10^{-10}\, f_0=4.57 \cdot 10^{-3} Hz }[/math] thus the satellite must use [math]\displaystyle{ f_0'=10.22999999543\,Mhz }[/math]. Notice that [math]\displaystyle{ \displaystyle f_0^' }[/math] is the frequency "emitted" by the satellite and [math]\displaystyle{ \displaystyle f_0 }[/math] is the one "received" on the terrestrial surface, i.e., an apparent increase of the frequency is of [math]\displaystyle{ 4.57 \cdot 10^{-3} Hz }[/math]. That is, the clock on satellite appear to run faster ([math]\displaystyle{ \simeq 38 \mu s/day }[/math]) than on ground [note: [math]\displaystyle{ \displaystyle \Delta f/f=\Delta T/T }[/math]]. This effect is corrected (in factory) decreasing the oscillating frequency of the satellite by this amount [math]\displaystyle{ 4.57 \cdot 10^{-3} Hz }[/math].
- ^ Note: Over the osculating orbit, [math]\displaystyle{ \sqrt{\mu a}\,e\sin E={\mathbf r} \cdot {\mathbf v} }[/math]. Thence, [math]\displaystyle{ \Delta_{rel}=- 2\, \frac{\mathbf{r} \cdot \mathbf{v}}{c^2}= -2\,\frac{\sqrt{\mu\, a}}{c^2} \, e\, \sin(E) }[/math], where [math]\displaystyle{ \displaystyle \mu }[/math] the (geocentric) gravitational constant, [math]\displaystyle{ \displaystyle c }[/math] the speed of light in a vacuum, [math]\displaystyle{ \displaystyle a }[/math] and [math]\displaystyle{ \displaystyle e }[/math] the semi-major axis and eccentricity of the osculating orbit and [math]\displaystyle{ \displaystyle E }[/math] the eccentric anomaly.
References
- ^ a b Ashby, N., 2003 Relativity in the Global Positioning System