If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
RAIM Fundamentals
| Fundamentals | |
|---|---|
| Title | RAIM Fundamentals |
| Edited by | GMV |
| Level | Basic |
| Year of Publication | 2011 |
Traditional RAIM techniques aim at computing protection levels for the GNSS navigation solution based on the standard deviation of the measurement noise, the measurement geometry and the maximum allowed probabilities of false alarm and missed detection.
Introduction
Traditional RAIM techniques[1][2] can be decomposed into the following main elements:
- FDE (fault detection and exclusion) , which can be further decomposed into:
- Fault detection: a process responsible for checking the consistency of the measurements, usually by means of a statistical hypothesis test on the residuals of a least squares position estimation, in which the null hypothesis implies that there are no faulty measurements. If the test fails (in the sense that the null hypothesis is rejected), then a fault detection is declared.
- Fault exclusion: this function is called only if the fault detection function above declares detection. Its purpose is to decide which measurement or group of measurements is more likely to be responsible for the fault detected in the previous step and reject the affected measurements so that they are not used in the navigation solution. Some iterative implementations would then call again the fault detection function to make sure that no further detections occur. The sequence fault detection –fault exclusions may be called iteratively until no further detection occurs, and hence no other exclusions are required.
- Position and Protection Level (PL) computation: position (together with a consistent protection level) is re-computed using those measurements that have passed the FDE test successfully. The said protection level can be computed in different ways depending on the assumptions it relies on. Classic RAIM techniques (designed for the civil aviation framework in a GPS-only scenario) assume that only one measurement can be faulty at a given time, but these techniques can be (and have been) generalized to the cases of simultaneous faults. The assumption on the number of faulty measurements that can exist is, of course, linked to the performance level of the FDE mechanism (as well as the quality of the inputs).
Classic RAIM Approach
Depending on the particular geometry of the satellites used in the navigation solution (i.e. the ones corresponding to those measurements which have passed the fault detection test), the position estimate may be more sensitive to errors in some satellite measurements than others. A one meter measurement error in a given satellite might cause a two meters position error while the same one-meter measurement error in another satellite might cause only a half meter position error. Likewise, different satellite ranging errors might contribute differently to the fault detection statistic (i.e. to the root mean square of the individual satellites’ residuals). In both cases, the contribution of each particular satellite is linear (when all other measurements are perfect, i.e. have no errors).
Hence, for any given satellite, the relation between its contribution to the test statistic and its contribution to position error is also linear: doubling the contribution to the test statistic would also double the contribution to position error (again, assuming that all other measurements are perfect, and hence yield a null contribution to both the test statistic and the position error).
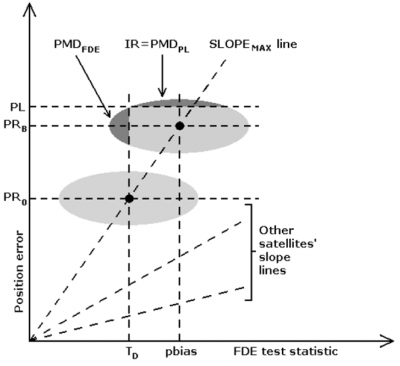
The figure schematically represents how RAIM protection levels are computed. The horizontal axis represents the value of the test statistic used in the FDE test (usually the root mean square of all individual satellites' estimation residuals). The vertical axis represents the absolute position error (e.g. in meters). Furthermore, each satellite is associated to a straight line representing the amount of position error induced by a given size of the test statistic caused by a ranging error from that satellite in absence of ranging errors from all other satellites. Assuming that, at the most, one faulty measurement remains after the FDE test, the protection level is computed such as to cover the situation with the most impact in the position error, i.e. the situation where the faulty measurement is the one corresponding to the satellite with the maximum slope.
In the FDE test, the test statistic (root mean square of residuals) is compared with a threshold [math]\displaystyle{ T_D }[/math]. If the threshold is not exceeded, then the test is declared successful. However, this does not necessarily imply that all measurements are fault-free. There might be some faulty measurement whose contribution to the test statistic is small enough for the test to pass. Clearly, the most dangerous measurement to be faulty would be the one that produces the largest position error without being detected by the FDE test, that is, the one producing the largest position error with a fixed contribution to the estimation residual or, in other words, the one with the maximum slope in the figure. Since the test has succeeded (otherwise we would not be computing the protection level), the test statistic is not larger than [math]\displaystyle{ T_D }[/math], and if only one measurement is faulty and all other measurements are perfect, then the resulting position error would be, at the most, that corresponding to a fault in the worst satellite (the one with maximum slope) when the test statistic reaches its maximum [math]\displaystyle{ T_D }[/math]. Therefore, one would be tempted to set the protection level at [math]\displaystyle{ PR_0 }[/math].
But now we have to take into account that the other (non-faulty) measurements are not perfect, but are subject of errors which follow some (known) fault-free statistics. In classic RAIM, it is assumed that fault-free measurement errors follow a zero mean Gaussian distribution.
Fault-free error statistics are schematically represented in the figure as a gray ellipse which shows that, even when the FDE test passes (left half of the lower ellipse) it can be the case that position error exceeds [math]\displaystyle{ PR_0 }[/math] (upper left quarter of the lower ellipse). Actually, the left half of the ellipse represents FDE misdetection probability, since the points in that region represent situations in which the test passes, but the measurement with maximum slope is faulty. Please note that just an infinitesimal increment of that error would be above the detection threshold, but due to the compensating effects of other satellites’ errors, the test statistic would not exceed the threshold and the fault would not be detected. Actually, since the ellipse is symmetric, this situation would imply an FDE misdetection rate of 50%. Since FDE misdetection rate is an input to the design (and is usually much smaller than 50%), we have to move along the maximum slope line up to the point in which the probability mass on the left of [math]\displaystyle{ T_D }[/math] is smaller than or equal to the target FDE misdetection rate, [math]\displaystyle{ PMD_{FDE} }[/math], represented with the upper ellipse in the figure. The displacement in the horizontal axis that is needed to reach this point is called [math]\displaystyle{ p_{bias} }[/math] in RAIM literature, and can be computed using the (supposedly known) statistics of the fault-free ranging errors.
At this point, if [math]\displaystyle{ PR_B }[/math] would be used as the protection level, then the upper half of the new ellipse would still represent position errors above the protection level. The target Integrity Risk (IR) is then used by the algorithm to displace the final protection level upwards, to a value PL, so that the probability mass (of the fault-free ranging error statistic represented by the ellipse) left above PL is smaller than or equal to the target integrity risk (also called protection level misdetection rate, [math]\displaystyle{ PMD_{PL} }[/math], by some authors).
So, one can see that there are two main ingredients in the computation of a RAIM protection level:
- one related to the possible presence of faulty measurements
- another one related to the error statistics of the remaining (non-faulty) measurements. However, it relies on the assumption that the fault-free error statistics are known, and, in practice, they are usually fed as configuration parameters to the RAIM function.
These ideas can be generalized to a K-fault RAIM technique in which the protection level is computed assuming that up to K measurements can be faulty at a given time. The only difference would be in the way that the maximum slope is computed. Instead of searching for the satellite with the maximum slope, one has to search for a linear combination of satellites that yield the maximum slope.
Related articles
References
- ^ R. G. Brown et al., “GPS RAIM: Calculation of threshold and protection radius using chi-square methods-a geometric approach”, in Global Positioning System: Inst. Navigat., 1997, vol. V, pp. 155-179.
- ^ R. G. Brown, “Solution of the two-failure GPS RAIM problem under worst-case bias conditions: parity space approach,” Journal of The Institute of Navigation, vol. 44, no. 4, pp. 425-431, 1998.