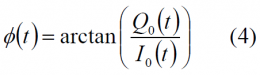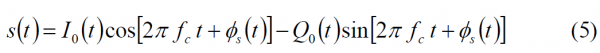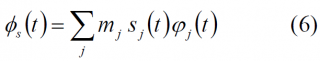If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Quadrature Product Sub-carrier Modulation
| Fundamentals | |
|---|---|
| Title | Quadrature Product Sub-carrier Modulation |
| Author(s) | J.A Ávila Rodríguez, University FAF Munich, Germany. |
| Level | Advanced |
| Year of Publication | 2011 |
The quadrature product sub-carrier modulation (QPSM) enables the transmission of a quadrature multiplexed carrier modulation with one or more sub-carrier signals in the same constant envelope waveform as shown in [P.A. Dafesh, 1999][1] and [P.A. Dafesh et al., 2006][2]. Moreover, in its generalized form, QPSM is capable of applying sub-carrier modulation to already existing systems with Quadrature Phase Shift Keying (QPSK) or Minimum Shift Keying (MSK). In fact, one of its main advantages is that it can easily introduce new additional spread signals with excellent spectral isolation to those already in the band, using the same transmitter power amplifier. This is accomplished using multiple rate product codes that cause minimal interference to the existing ones. Finally, the power control and energy distribution between the carrier and sub-carrier signals can be accomplished selecting the desired modulation index.
In the next lines we show how the QPSM modulation can be represented mathematically. However, let us begin first with a simplified model. Let us assume a pair of quadrature components [math]\displaystyle{ I_0 }[/math] and [math]\displaystyle{ Q_0 }[/math] onto a carrier signal as follows,
where [math]\displaystyle{ f_c }[/math] denotes the carrier frequency. As we can clearly recognize, the magnitude is constant and can be expressed as follows [S. Butman and U. Timor, 1972][3]:
where
and
From the equations above we can recognize that the resulting composite signal has a constant magnitude [math]\displaystyle{ A_0 }[/math] and does not depend on time as long as [math]\displaystyle{ I_0^2\left(t\right) }[/math] and [math]\displaystyle{ Q_0^2\left(t\right) }[/math] do not vary, what is always satisfied if I0 and Q0 are binary sequences.
Indeed this is the basic idea of the QPSM modulation. If we generalize now this principle, we can further add new signals modulating the phase part according to the following approach [S. Butman and U. Timor, 1972] [3]:
with
where
- [math]\displaystyle{ m_j }[/math] is the modulation index of the j-th signal. It determines the power allocation of each component,
- [math]\displaystyle{ s_j\left(t\right) }[/math] is the j-th signal to modulate. It can be expressed as the product of the respective data message and the PRN code.
- and [math]\displaystyle{ \phi_j\left(t\right) }[/math] is the periodic sub-carrier, which may be any regular signal as for example sine, square or triangular, for example.
It is trivial to see that the envelope also remains constant in this modulated carrier signal. Moreover, the sub-carrier signal can be made up of many components being the limit only the phase noise that appears when the states of the constellation come too close to each other, as we will see later. Furthermore, the model is not only valid for binary sequences. In fact, the periodic sub-carrier could adopt any form in principle as long as it is regular. This is very important, because the Composite Binary Coded Symbols (CBCS) and Composite BOC (CBOC) signals are not binary.
The conventional sub-carrier modulation presents so-called cross-product inter-modulation components which can be considered as signal losses, resulting thus in a loss of efficiency. The conventional constant envelope Sub-carrier Modulation is used today on the Space Ground Link Subsystem (SGLS) and other terrestrial and space systems as shown by [P.A. Dafesh et al., 1999][1], [Philco-Ford Corp., 1968],[4] [J.K. Holmes, 1982][5] and [M. M. Shihabbi et al., 1994][6]. A generalization of the Sub-carrier modulation that has gained in interest over the past years is the Coherent Adaptive Sub-Carrier, which is presented in the following chapter.
Finally, it is important to note that the spectral separation of the different signals to modulate depends on the sub-carrier signal in particular allowing thus for spectral control as desired.
References
- ^ a b [P.A. Dafesh et al., 1999] P.A. Dafesh, S. Lazar, and T. Nguyen, Coherent Adaptive Sub-carrier Modulation (CASM) for GPS Modernization, Proceedings of the National Technical Meeting of the Institute of Navigation, ION-NTM 1999, January 1999, San Diego, California, USA.
- ^ [P.A. Dafesh et al., 2006] P.A. Dafesh, Nguyen, M. Tien, Quadrature product sub-carrier modulation system, Patent US 7120198, Granted 10 October 2006.
- ^ a b [S. Butman and U. Timor, 1972] S. Butman and U. Timor , Interplex – An efficient Multichannel PSK/PM Telemetry System, Proceedings of IEEE Transaction on Communications, Volume 20, No. 3 – June 1972
- ^ [Philco-Ford Corp., 1968] Philco-Ford Corp., System Design Analysis, Space-Ground Subsystem. Ground Station, System Analysis Summary Report, Vol. I, November 15, 1968.
- ^ [J.K. Holmes, 1982] J.K. Holmes, Coherent Spread Spectrum Systems, Publisher John Wiley and Sons, Inc. New York, New York, USA.
- ^ [M. M. Shihabbi et al., 1994] M. M. Shihabbi, T. M. Nguyen and S. M. Hinedi, A Comparison of Telemetry Signals in the Presence and Absence of a Sub-carrier, IEEE Transaction on Electromagnetic Compatibility, Vol. 36, No. 1, February, 1994.
Credits
The information presented in this NAVIPEDIA’s article is an extract of the PhD work performed by Dr. Jose Ángel Ávila Rodríguez in the FAF University of Munich as part of his Doctoral Thesis “On Generalized Signal Waveforms for Satellite Navigation” presented in June 2008, Munich (Germany)