If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Precise GNSS Satellite Coordinates Computation
| Fundamentals | |
|---|---|
| Title | Precise GNSS Satellite Coordinates Computation |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Intermediate |
| Year of Publication | 2011 |
Precise orbits and clocks for GPS and GLONASS satellites can be found at the International GNSS Service (IGS) web server [footnotes 1].
These products are in the public domain and free of charge for all users. They are available in ASCII files, providing precise orbits & clock files with a sample rate of 15 minutes, as well as precise clock files with 5 minutes and 30 seconds sample rate in SP3 format.
Table 1 summarizes the different products available, their accuracy, latency and sampling rate. It must be pointed out that IGS has adopted the International Terrestrial Reference System (ITRS) as its reference system. Thence, IGS products are referred to this system.
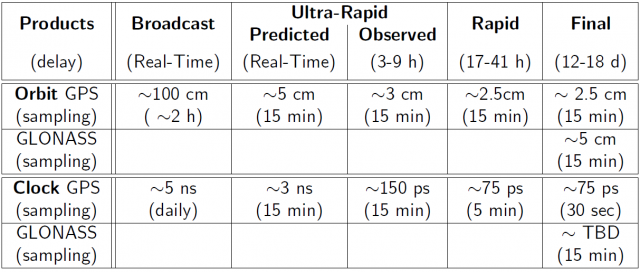 Table 1: IGS orbits and clocks products: RMS accuracy, latency and sampling (source: http://igscb.jpl.nasa.gov/components/prods.html, 2009).
Table 1: IGS orbits and clocks products: RMS accuracy, latency and sampling (source: http://igscb.jpl.nasa.gov/components/prods.html, 2009).
Some centres provide also GPS satellite clocks with 5 seconds sampling rate, like files obtained from the CDDIS site [footnotes 2]. Please bear in mind that orbits and clock files must be consistent (i.e., they must come from the same centre). Therefore, CODE clocks must be used with CODE orbits, and not with JPL nor EMR products, for instance.
The ANTenna EXchange format (ANTEX) files, along with other additional useful information on IGS antennas [footnotes 3].
The satellite coordinates between epochs can be computed by polynomial interpolation. A 10 order polynomial is enough for a centimetre level of accuracy with 15 minutes data. Clocks with sampling rate of 30 seconds or higher can be interpolated with a 1 order polynomial with few centimetres of accuracy. Clocks with lower sampling rate should not be interpolated, because clocks perform as random walk processes.
As an example of polynomial interpolation, the Lagrange method is presented as follows:
Given a table of values [math]\displaystyle{ (x_i,y_i) }[/math], [math]\displaystyle{ i=1,\dots,n }[/math], the interpolated value [math]\displaystyle{ y\simeq P_n(x) }[/math] at a given [math]\displaystyle{ x }[/math] can be computed as:
- [math]\displaystyle{ \begin{array}{lll} P_n(x)&=&\displaystyle \sum_{i=1}^n{y_i \frac{\prod_{j\neq i}{(x-x_j)}}{\prod_{j\neq i}{(x_i-x_j)}}}=\\ &=& y_1\displaystyle \frac{x-x_2}{(x_1-x_2)} \cdots \frac{x-x_n}{(x_1-x_n)}+\cdots\\ & &+y_i\displaystyle \frac{x-x_1}{(x_i-x_1)} \cdots \frac{x-x_{i-1}}{(x_i-x_{i-1})}\frac{x-x_{i+1}}{(x_i-x_{i+1})}\cdots \frac{x-x_n}{(x_i-x_n)}+\cdots\\ & & +y_n \displaystyle \frac{x-x_1}{(x_n-x_1)} \cdots\frac{x-x_{n-1}}{(x_n-x_{n-1})} \end{array} \qquad \mbox{(1)} }[/math]
Notes
- ^ Other useful sites with data products and information are the CDDIS at (ftp://cddis.gsfc.nasa.gov/gps) and (ftp://cddis.gsfc.nasa.gov/glonass).
- ^ ftp://cddis.gsfc.nasa.gov/pub/gps/products/.
- ^ https://kb.igs.org/hc/en-us/articles/203864436-Antenna-Files-Information.
