If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
APPROVED
Not Approved
Vicente.Navarro approved this page 14 July
14 July
Perturbed Motion
Jump to navigation
Jump to search
| Fundamentals | |
|---|---|
| Title | Perturbed Motion |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Intermediate |
| Year of Publication | 2011 |
The two-body problem is only a first approximation to the real case. In practice, an additional set of accelerations or disturbing terms, must be added due to:
- 1. Non-sphericity of the Earth and non-homogeneous mass distribution:
- As commented before, the shape of the Earth can be approximated by an ellipsoid, with equatorial radius about [math]\displaystyle{ 20\,km }[/math] larger than polar radius. On the other hand, the density is not uniform and the gravitational force depends on the latitude and longitude besides the radial distance. Thus, the Earth potential [footnotes 1] can be represented by a spherical harmonic expansion [Hofmann-Wellenhof et al., 2008] [1] like:
- [math]\displaystyle{ \begin{array}{ll} V= & \displaystyle \frac{\mu}{r}\left[ 1- \displaystyle \sum_{n=2}^{\infty}{\left(\frac{a_e}{r}\right)^n J_n\; P_n(\sin \phi)} \right .\\ & + \left. \displaystyle \sum_{n=2}^{\infty}{\displaystyle \sum_{m=1}^{n}{\left(\frac{a_e}{r}\right)^n \left[ C_{nm} \cos m\lambda + S_{nm} \sin m\lambda \right ] P_{nm}(\sin \phi)}}\right ] \end{array} \qquad \mbox{(1)} }[/math]
- where [math]\displaystyle{ \displaystyle a_e }[/math] is the semi-major axis of the Earth, [math]\displaystyle{ \displaystyle r }[/math] is the geocentric distance of the satellite, and [math]\displaystyle{ \displaystyle \phi }[/math], [math]\displaystyle{ \displaystyle \lambda }[/math] are its latitude and longitude. The parameters [math]\displaystyle{ \displaystyle J_n }[/math], [math]\displaystyle{ \displaystyle C_{nm} }[/math], [math]\displaystyle{ \displaystyle S_{nm} }[/math] denote the zonal ([math]\displaystyle{ \displaystyle m=0 }[/math]) and tesseral ([math]\displaystyle{ \displaystyle m \neq 0 }[/math] ) coefficients of the harmonic development known from an Earth model. [math]\displaystyle{ \displaystyle P_n }[/math] and [math]\displaystyle{ \displaystyle P_{nm} }[/math] are the Legendre polynomials and the associated Legendre functions, respectively.
- The even-degree zonal coefficients produce primary secular variations of the orbital parameters, and the odd-degree zonal produce long-period perturbations. The tesseral coefficients produce short -periodic perturbations.
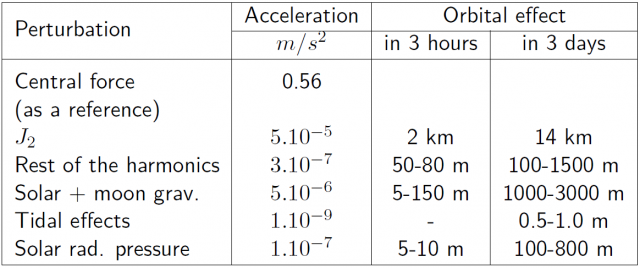
- The term with coefficient [math]\displaystyle{ \displaystyle J_2 }[/math] in (1), the harmonic coefficient of second order and degree zero, essentially models the ellipsoidal shape of the Earth (with homogeneous density). It is smaller, by a factor of [math]\displaystyle{ 10^4 }[/math], than the acceleration due to the spherical Earth with uniform density (i.e., [math]\displaystyle{ \displaystyle \nabla (\mu/r)=-\frac{\mu}{r^3}r }[/math]). On the other hand, this term is approximately three orders of magnitude larger than the other coefficients (see table 3). Taking only this term in the potential, the previous expression becomes:
- [math]\displaystyle{ V(r,\phi,\lambda)=\frac{\mu}{r}\left[1+\frac{1}{2}\left(\frac{a_e}{r}\right)^2 J_2\;\;(1-3\sin^2 \phi) \right] \qquad \mbox{(2)} }[/math]
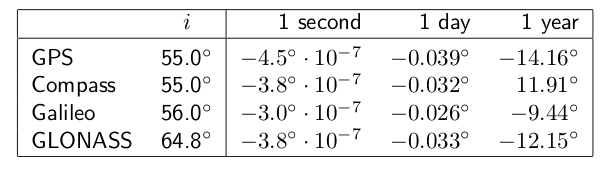
- The oblateness of the Earth ([math]\displaystyle{ \displaystyle J_2 }[/math]) produces two effects: First, a torque which rotates the satellite's orbit in the equatorial plane, producing a nodal regression [math]\displaystyle{ \displaystyle \frac{d \Omega}{dt} }[/math]. This is a secular effect (i.e., timely cumulative) which depends upon the inclination of the orbit. It is zero for a polar orbit and maximum for an equatorial orbit. Next table shows the rate of change for the GPS, BeiDou (MEO), Galileo and GLONASS satellites. ([Cojocaru, 2009] [2])
- The second effect of the non-central geo-potential ([math]\displaystyle{ \displaystyle J_2 }[/math]) produces a rotation of the perigee [math]\displaystyle{ \displaystyle \frac{d \omega}{dt} }[/math] (i.e., a rotation of the major axis in the orbital plane).
- This second harmonic of the geopotential ([math]\displaystyle{ \displaystyle J_2 }[/math]) does not produce secular perturbations in the elements [math]\displaystyle{ \displaystyle a }[/math], [math]\displaystyle{ \displaystyle e }[/math] and [math]\displaystyle{ \displaystyle i }[/math].
- 2. The presence of other celestial bodies, foremost, the sun and the moon:
- The gravitational field of sun and moon act as perturbing forces on the satellites, being the moon the body producing the largest effects [footnotes 2]. These gravitational forces also produce tides deforming the shape of the Earth and affecting its gravitational potential. Nevertheless, these tidal effects produce on GNSS satellites accelerations at the order of [math]\displaystyle{ \displaystyle 10^{-9} m/s^2 }[/math], which are three orders of magnitude lower than the moon and solar gravitational acceleration (see Table 3).
- 3. Solar radiation pressure:
- This is produced by the photons impacting on the satellite surface and mainly depends on the reflective properties and the area-to-mass ratio of the satellite. It also depends on an eclipse factor, being zero when the satellite is in the Earth's shadow. The effect of solar radiation pressure on a satellite orbit is very difficult to model, and some contribution is estimated as stochastic acceleration parameters in the filter during the orbit estimation.
- Note that although the sun and the moon gravitational effects and the non-gravitational solar radiation pressure perturbing accelerations appear very small, their accumulated effect can produce significant changes in the GNSS satellites orbits over a large period of time. Table 3 (from [Seeber, 1993] [3]) shows the different perturbation magnitudes and their effect over GPS orbits.
References
- ^ [Hofmann-Wellenhof et al., 2008] Hofmann-Wellenhof, B., Lichtenegger, H., K. and Wasle, E., 2008. GNSS - Global Navigation Satellite Systems.. Springer-Verlag, Wien, Austria
- ^ [Cojocaru, 2009] Cojocaru, S., 2009. GPS-GLONASS-GALILEO: A Dynamical Comparison. The Journal of Navigation, The Royal Institute of Navigation, UK. 62, pp. 135-150.
- ^ [Seeber, 1993] Seeber, G., 1993. Satellite Geodesy: Foundations, Methods, and Applications. Walter de Gruyter & Co., Berlin, Germany.
Notes
- ^ In equation [math]\displaystyle{ \mathbb{\mathbf {\ddot r}}+\displaystyle\frac{\mu}{r^3}\mathbb{\mathbf r}=\mathbb{\mathbf 0} }[/math], the term [math]\displaystyle{ -\frac{\mu}{r^3}\mathbb{\mathbf r}=\nabla (\mu/r) }[/math] corresponds to the acceleration from a potential produced by a spherical Earth with uniform density, see also equation (1) in GNSS Broadcast Orbits.
- ^ Note that, although being the sun much more massive than the moon, it is also much more farther away, and the gravitational effect is proportional to the inverse of the square of the distance.