If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Mapping of Niell
| Fundamentals | |
|---|---|
| Title | Mapping of Niell |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Advanced |
| Year of Publication | 2011 |
A mapping function that does not require surface meteorology measurements, but provides comparable accuracy and precision to others that requires such data is presented in [Niell, 1996][1]. This mapping only uses the receiver geographic location and measurement time as inputs.
The Niell's mapping involves two different obliquity factors, for the dry and wet components, which are computed from the equations (1) to (4), where [math]\displaystyle{ (E) }[/math] is the elevation of ray and [math]\displaystyle{ (H) }[/math] is the receiver height, in kilometres:
Hydrostatic mapping function:
- [math]\displaystyle{ \begin{array}{l} M_{dry}(E,H)= m(E,a_d,b_d,c_d)+ \Delta m(E,H)\\ \qquad\mbox{with}\\ \Delta m(E,H)= \left[ \frac{1}{sin E} - m(E,a_{ht},b_{ht},c_{ht}) \right ] \cdot H \end{array} \qquad\mbox{(1)} }[/math]
Wet Mapping Function:
- [math]\displaystyle{ M_{wet}(E)= m(E,a_w,b_w,c_w) \qquad\mbox{(2)} }[/math]
- where, [math]\displaystyle{ m(E,a,b,c) }[/math] is the [Marini, 1972][2] mapping normalised to unity at zenith:
- [math]\displaystyle{ m(E,a,b,c)= \frac{1+\frac{a}{1+\frac{b}{1+c}}}{\sin E+\frac{a}{\sin E+\frac{b}{\sin E+c}}} \qquad\mbox{(3)} }[/math]
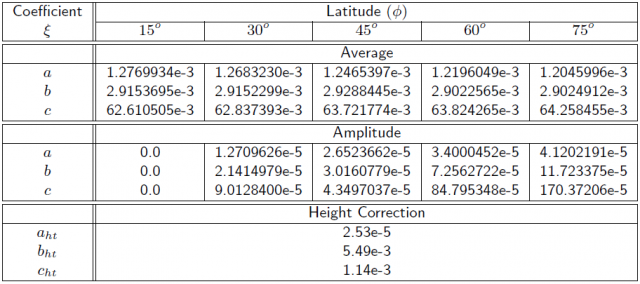
- The Hydrostatic parameters [math]\displaystyle{ a_d }[/math], [math]\displaystyle{ b_d }[/math], [math]\displaystyle{ c_d }[/math] are time [math]\displaystyle{ (t) }[/math] and latitude ([math]\displaystyle{ \Phi) }[/math] dependent parameters given by:
- [math]\displaystyle{ \xi(\phi,t)=\xi_{_{avg}}(\phi)-\xi_{_{amp}}(\phi) \cos \left ( 2\pi \frac{t-T_0}{365.25} \right ) \qquad\mbox{(4)} }[/math]
where, [math]\displaystyle{ t }[/math] is the time from January [math]\displaystyle{ 0.0 }[/math], in days, and [math]\displaystyle{ T_0 }[/math] is taken as DoY [math]\displaystyle{ 28 }[/math] (i.e., [math]\displaystyle{ T_0=28 }[/math]). The parameters [math]\displaystyle{ \xi_{_{avg}}(\phi_i) }[/math] and [math]\displaystyle{ \xi_{_{amp}}(\phi_i) }[/math] are linearly interpolated from table 1 between the nearest [math]\displaystyle{ \xi(\Phi_i) }[/math]. The [math]\displaystyle{ a_{ht} }[/math], [math]\displaystyle{ b_{ht} }[/math], [math]\displaystyle{ c_{ht} }[/math] are taken directly from the same table 1.
- The wet parameters [math]\displaystyle{ a_w }[/math], [math]\displaystyle{ b_w }[/math], [math]\displaystyle{ c_w }[/math] are latitude dependent and are linearly interpolated from table 2 between the nearest [math]\displaystyle{ \xi(\Phi_i) }[/math].
References
- ^ [Niell, 1996] Niell, A., 1996. Global mapping functions for the atmosphere delay at radio wavelengths. Journal of Geophysical Research. 101, pp. 3227-3246.
- ^ [Marini, 1972] Marini, J., 1972. Correction of Satellite tracking data for an arbitrary Tropospheric Pro_le. Radio Science. 7(2), pp. 223-231.