If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
ICRF to CEP
| Fundamentals | |
|---|---|
| Title | ICRF to CEP |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Advanced |
| Year of Publication | 2011 |
To transform coordinates from ICRF to the CEP it is necessary to correct the Precession and Nutation effects. This transformation is performed by a composite of rotations that can done by two orthogonal matrices [math]\displaystyle{ {\mathbf P} }[/math] and [math]\displaystyle{ {\mathbf N} }[/math] as follows:
- [math]\displaystyle{ {\mathbf r}_{CEP}={\mathbf N}\; {\mathbf P}\; {\mathbf r}_{ICRF} \qquad \mbox{(1)} }[/math]
- Precession Matrix: [math]\displaystyle{ {\mathbf P} }[/math]
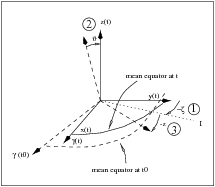
- In figure 1 are indicated all the angles involved and the rotations needed in this transformation:
- [math]\displaystyle{ \gamma (t) }[/math] stands for the mean vernal equinox at the observation time [math]\displaystyle{ t }[/math] and [math]\displaystyle{ \gamma (t_0) }[/math] is the mean vernal equinox at the reference epoch [math]\displaystyle{ t_0 }[/math] (i.e., J2000).
- The operations to perform are:
- [math]\displaystyle{ \begin{array}{c} {\mathbf P}={\mathbf R}_{3}\left( -z\right) \; {\mathbf R}_{2}\left( \vartheta \right) \; {\mathbf R}_{3}\left( -\zeta \right) = \\ \\ \\ =\left[\begin{array}{ccc}\cos (-z) & \sin (-z) & 0 \\ -\sin (-z) & \cos (-z) & 0 \\ 0 & 0 & 1\end{array}\right] \; \left[ \begin{array}{ccc}\cos \vartheta & 0 & -\sin \vartheta \\ 0 & 1 & 0 \\ \sin \vartheta & 0 & \cos \vartheta \end{array}\right] \; \left[ \begin{array}{ccc}\cos (-\zeta) & \sin (-\zeta) & 0 \\ -\sin (-\zeta) & \cos (-\zeta) & 0 \\ 0 & 0 & 1\end{array}\right] = \\ \\ \\ =\left[ \begin{array}{ccc}\begin{array}{c}\cos z\; \cos \vartheta \; \cos \zeta - \\ -\sin z\; \sin \zeta \end{array}& \begin{array}{c}-\cos z\; \cos \vartheta \; \sin \zeta - \\ -\sin z\; \cos \zeta \end{array}& -\cos z\; \sin \vartheta \\ \begin{array}{c}\sin z\; \cos \vartheta \; \cos \zeta + \\ +\cos z\; \sin \zeta \end{array}& \begin{array}{c}-\sin z\; \cos \vartheta \; \sin \zeta + \\ +\cos z\; \cos \zeta \end{array}& -\sin z\sin \vartheta \\ \sin \vartheta \; \cos \zeta & -\sin \vartheta \; \sin \zeta & \cos\vartheta \end{array}\right] \\ \end{array} \qquad \mbox{(2)} }[/math]
The first rotation ([math]\displaystyle{ R_3\left( -\zeta \right) }[/math]) is a displacement of the y(t) and x(t) axis, by means of a z(t) axis rotation, to the intersection between the mean equator at the reference epoch [math]\displaystyle{ t_0 }[/math] (J2000) and the mean equator at the observation epoch [math]\displaystyle{ t }[/math] (marked in the figure by an I). The second one ([math]\displaystyle{ R_2\left( \vartheta \right) }[/math]) is a rotation over the axis y(t) and its objective is to match the two equators involved in these coordinate system. The last rotation ([math]\displaystyle{ R_3\left(-z\right) }[/math]) is over z(t) axis again, in order to overlap the two coordinate systems. The angles involved can be computed following the expressions (IAU 1976 Precession Model [footnotes 1]):
- [math]\displaystyle{ \begin{array}{c} z=2306_{\cdot}^{\prime \prime}2181 \; T+1_{\cdot}^{\prime \prime}09468 \; T^2+0_{\cdot}^{\prime \prime}018203 \; T^3 \\ \vartheta =2004_{\cdot}^{\prime \prime}3109 \; T-0_{\cdot}^{\prime \prime}42665 \; T^2-0_{\cdot}^{\prime \prime}041833 \; T^3 \\ \zeta =2306_{\cdot}^{\prime \prime}2181\; T+0_{\cdot}^{\prime \prime}30188 \; T^2+0_{\cdot}^{\prime \prime}017998 \; T^3 \end{array} \qquad \mbox{(3)} }[/math]
where [math]\displaystyle{ T }[/math] is the time expressed in Julian centuries (see equation (17) in Transformations between Time Systems) between the reference epoch J2000.0 and the epoch [math]\displaystyle{ t }[/math] of observation. An important note to point out is that the time [math]\displaystyle{ t }[/math] must be expressed in TDB scale because, as said in previous sections, all computations related to solar system planet orbits and mechanics must be expressed in this scale.
- Nutation Matrix: [math]\displaystyle{ {\mathbf N} }[/math]
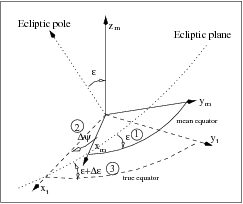
- This matrix is similar to that studied in the previous case. In Figure 2 are described the steps to perform the Nutation correction. The objective of this rotation is to match the mean coordinates (labelled with "[math]\displaystyle{ m }[/math]") with the true coordinates (labelled with "[math]\displaystyle{ t }[/math]"), this operation is made through the ecliptic plane as showed in this graphic.
- In this case the Nutation Matrix is defined as:
- [math]\displaystyle{ \begin{array}{c} \begin{array}{c} {\mathbf N}={\mathbf R}_{1}\left( -(\varepsilon +\Delta \varepsilon )\right) \; {\mathbf R}_{3}\left( -\Delta \psi \right) \; {\mathbf R}_{1}\left( \varepsilon \right) = \end{array}\\ \\ \begin{array}{c} =\left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos -(\varepsilon +\Delta \varepsilon ) & \sin -(\varepsilon +\Delta \varepsilon ) \\ 0 & -\sin -(\varepsilon +\Delta \varepsilon ) & \cos -(\varepsilon +\Delta \varepsilon ) \end{array} \right] \; \left[ \begin{array}{ccc} \cos -\Delta \psi & \sin -\Delta \psi & 0 \\ -\sin -\Delta \psi & \cos -\Delta \psi & 0 \\ 0 & 0 & 1 \end{array} \right] \; \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & \cos \varepsilon & \sin \varepsilon \\ 0 & -\sin \varepsilon & \cos \varepsilon \end{array} \right] = \\ \\ \\ =\left[ \begin{array}{ccc} \cos \Delta \psi & -\cos \varepsilon \; \sin \Delta \psi & -\sin \varepsilon \; \sin \Delta \psi \\ \cos (\varepsilon +\Delta \varepsilon )\; \sin \Delta \psi & \begin{array}{c} \cos (\varepsilon +\Delta \varepsilon )\; \cos \varepsilon \; \cos \Delta \psi + \\ +\sin (\varepsilon +\Delta \varepsilon )\; \sin \varepsilon \end{array} & \begin{array}{c} \cos (\varepsilon +\Delta \varepsilon )\; \sin \varepsilon \; \cos \Delta \psi - \\ -\sin (\varepsilon +\Delta \varepsilon )\; \cos \varepsilon \end{array} \\ \sin (\varepsilon +\Delta \varepsilon )\; \sin \Delta \psi & \begin{array}{c} \sin (\varepsilon +\Delta \varepsilon )\; \cos \varepsilon \; \cos \Delta \psi - \\ -\cos (\varepsilon +\Delta \varepsilon )\; \sin \varepsilon \end{array} & \begin{array}{c} \sin (\varepsilon +\Delta \varepsilon )\; \sin \varepsilon \; \cos \Delta \psi + \\ +\cos (\varepsilon +\Delta \varepsilon )\; \cos \varepsilon \end{array} \end{array} \right] \\ \end{array} \end{array} \qquad \mbox{(4)} }[/math]
- The first rotation ([math]\displaystyle{ R_{1}\left( \varepsilon \right) }[/math]), over [math]\displaystyle{ x_m }[/math] axis, puts the mean equator in the ecliptic plane. The second one ([math]\displaystyle{ R_{3}\left(-\Delta \psi \right) }[/math]), over the [math]\displaystyle{ z_m }[/math] axis, matches the true equinox with the mean one and, at last. The third rotation ([math]\displaystyle{ R_{1}\left( -(\varepsilon +\Delta \varepsilon )\right) }[/math]), over the [math]\displaystyle{ x_m }[/math] axis again, fits the mean equator into the true one. The parameters involved in this matrix can be computed as (1980 IAU Nutation model):
- [math]\displaystyle{ \begin{array}{c} \varepsilon =23^o26^{\prime }21_{\cdot}^{\prime \prime}448-46_{\cdot}^{\prime \prime}8150\; T-0_{\cdot}^{\prime \prime}00059\; T^2+0_{\cdot}^{\prime \prime}001813\; T^3 \\ \\ \Delta \psi = \sum_{j=1}^N\left[ \left( A_{0j}+A_{1j}\; T\right) \; \sin \left( \sum_{i=1}^5 k_{ji}\; \alpha _i\right) \right] \\ \\ \Delta \varepsilon =\sum_{j=1}^N\left[ \left( B_{0j}+B_{1j}\; T\right) \; \cos \left( \sum_{i=1}^5 k_{ji}\; \alpha _i\right) \right] \end{array} \qquad \mbox{(5)} }[/math]
where the parameters [math]\displaystyle{ A_{0j} }[/math], [math]\displaystyle{ A_{1j} }[/math], [math]\displaystyle{ B_{0j} }[/math], [math]\displaystyle{ B_{1j} }[/math] and [math]\displaystyle{ k_{ji} }[/math] are listed in table 2. The parameters [math]\displaystyle{ \alpha _i }[/math] are time dependant (just as [math]\displaystyle{ \varepsilon }[/math]) and are computed as:
- Moon's mean anomaly
- [math]\displaystyle{ \alpha_1=l=485\,866_{\cdot}^{\prime \prime}733+(1\,325^r+715\,922_{\cdot}^{\prime \prime}633)\; T+31_{\cdot}^{\prime \prime}310\; T^2+0_{\cdot}^{\prime \prime}064\; T^3 \qquad \mbox{(6)} }[/math]
- Sun's mean anomaly
- [math]\displaystyle{ \alpha_2=l^{\prime }=1\,287\,099_{\cdot}^{\prime \prime}804+(99^r+1\,292\,581_{\cdot}^{\prime \prime}224)\; T-0_{\cdot}^{\prime \prime}577\; T^2-0_{\cdot}^{\prime \prime}012\; T^3 \qquad \mbox{(7)} }[/math]
- Moon's mean argument of latitude
- [math]\displaystyle{ \alpha_3=F=335\,778_{\cdot}^{\prime \prime}877+(1342^r+295\,263_{\cdot}^{\prime \prime}137)\; T-13_{\cdot}^{\prime \prime}257\; T^2+0_{\cdot}^{\prime \prime}011\; T^3 \qquad \mbox{(8)} }[/math]
- Moon's mean elongation from the sun
- [math]\displaystyle{ \alpha_4=D=1\,072\,261_{\cdot}^{\prime \prime}307+(1\,236^r+1\,105\,601_{\cdot}^{\prime \prime}328)\; T-6_{\cdot}^{\prime \prime}891\; T^2+0_{\cdot}^{\prime \prime}019\; T^3 \qquad \mbox{(9)} }[/math]
- Mean longitude of the ascending lunar node
- [math]\displaystyle{ \alpha_5=\Omega =450\,160_{\cdot}^{\prime \prime}280-(5^r+482\,890_{\cdot}^{\prime \prime}539)\; T+7_{\cdot}^{\prime \prime}455\; T^2+0_{\cdot}^{\prime \prime}008\; T^3 \qquad \mbox{(10)} }[/math]
the value [math]\displaystyle{ 1^r=360^o=1\,296\,000^{\prime \prime } }[/math] and [math]\displaystyle{ T }[/math] is the same as the one used to compute the precession matrix.
- Inverse Transformation
The inverse transformation from CEP to ICRF is done by applying the different rotations in inverse way.
- [math]\displaystyle{ \begin{array}{|r|c c c c c |r |r|}\hline Index & & & A_{coeff} & & & Period & A_i~~~~\\ i~~~ & k_{i1} & k_{i2} & k_{i3} & k_{i4} & k_{i5} & (days) & (\times 10^{-4}s) \\ \hline & & & & & & & \\ 1 & 1 & 0 & 2 & 2 & 2 & 5.64 & -0.024 \\ 2 & 2 & 0 & 2 & 0 & 1 & 6.85 & -0.040 \\ 3 & 2 & 0 & 2 & 0 & 2 & 6.86 & -0.099 \\ 4 & 0 & 0 & 2 & 2 & 1 & 7.09 & -0.051 \\ 5 & 0 & 0 & 2 & 2 & 2 & 7.10 & -0.123 \\ 6 & 1 & 0 & 2 & 0 & 0 & 9.11 & -0.039 \\ 7 & 1 & 0 & 2 & 0 & 1 & 9.12 & -0.411 \\ 8 & 1 & 0 & 2 & 0 & 2 & 9.13 & -0.993 \\ 9 & 3 & 0 & 0 & 0 & 0 & 9.18 & -0.018 \\ 10 & -1 & 0 & 2 & 2 & 1 & 9.54 & -0.082 \\ 11 & -1 & 0 & 2 & 2 & 2 & 9.56 & -0.197 \\ 12 & 1 & 0 & 0 & 2 & 0 & 9.61 & -0.076 \\ 13 & 2 & 0 & 2 & -2 & 2 & 12.81 & 0.022 \\ 14 & 0 & 1 & 2 & 0 & 2 & 13.17 & 0.025 \\ 15 & 0 & 0 & 2 & 0 & 0 & 13.61 & -0.299 \\ 16 & 0 & 0 & 2 & 0 & 1 & 13.63 & -3.208 \\ 17 & 0 & 0 & 2 & 0 & 2 & 13.66 & -7.757 \\ 18 & 2 & 0 & 0 & 0 & -1 & 13.75 & 0.022 \\ 19 & 2 & 0 & 0 & 0 & 0 & 13.78 & -0.338 \\ 20 & 2 & 0 & 0 & 0 & 1 & 13.81 & 0.018 \\ 21 & 0 & -1 & 2 & 0 & 2 & 14.19 & -0.024 \\ 22 & 0 & 0 & 0 & 2 & -1 & 14.73 & 0.047 \\ 23 & 0 & 0 & 0 & 2 & 0 & 14.77 & -0.734 \\ 24 & 0 & 0 & 0 & 2 & 1 & 14.80 & -0.053 \\ 25 & 0 & -1 & 0 & 2 & 0 & 15.39 & -0.051 \\ 26 & 1 & 0 & 2 & -2 & 1 & 23.86 & 0.050 \\ 27 & 1 & 0 & 2 & -2 & 2 & 23.94 & 0.101 \\ 28 & 1 & 1 & 0 & 0 & 0 & 25.62 & 0.039 \\ 29 & -1 & 0 & 2 & 0 & 0 & 26.88 & 0.047 \\ 30 & -1 & 0 & 2 & 0 & 1 & 26.98 & 0.177 \\ 31 & -1 & 0 & 2 & 0 & 2 & 27.09 & 0.435 \\ 32 & 1 & 0 & 0 & 0 & -1 & 27.44 & 0.534 \\ 33 & 1 & 0 & 0 & 0 & 0 & 27.56 & -8.261 \\ 34 & 1 & 0 & 0 & 0 & 1 & 27.67 & 0.544 \\ 35 & 0 & 0 & 0 & 1 & 0 & 29.53 & 0.047 \\ 36 & 1 & -1 & 0 & 0 & 0 & 29.80 & -0.055 \\ 37 & -1 & 0 & 0 & 2 & -1 & 31.66 & 0.118 \\ 38 & -1 & 0 & 0 & 2 & 0 & 31.81 & -1.824 \\ 39 & -1 & 0 & 0 & 2 & 1 & 31.96 & 0.132 \\ 40 & 1 & 0 & -2 & 2 & -1 & 32.61 & 0.018 \\ 41 & -1 & -1 & 0 & 2 & 0 & 34.85 & -0.086 \\ \hline \end{array} }[/math]
- Table 1: Earth rotation variations due to zonal tides [Yoder et al., 1981][1] (see IERS 96 Conventions). Components with period under 35 days. See also http://hpiers.obspm.fr/eop-pc/models/UT1/UT1R_tab.html
- [math]\displaystyle{ \begin{array}{|r|c c c c c|r |r r |r r|} \hline Index & & & A_{coeff} & & &Period & A_{0j} & A_{1j}& B_{0j} & B_{1j}\\ i~~~ & k_{i1} & k_{i2} & k_{i3} & k_{i4} & k_{i5} & (days) & \times 10^{-4}&\prime\prime & \times 10^{-4}&\prime \prime \\ \hline & & & & & & & & & & \\ 1 & 0 & 0 & 0 & 0 & 1 & -6798.4 & -171996.0 & -174.2 & 92025.0 & 8.9 \\ 2 & 0 & 0 & 2 & -2 & 2 & 182.6 & -13187.0 & -1.6 & 5736.0 & -3.1 \\ 3 & 0 & 0 & 2 & 0 & 2 & 13.7 & -2274.0 & -0.2 & 977.0 & -0.5 \\ 4 & 0 & 0 & 0 & 0 & 2 & -3399.2 & 2062.0 & 0.2 & -895.0 & 0.5 \\ 5 & 0 & -1 & 0 & 0 & 0 & -365.3 & -1426.0 & 3.4 & 54.0 & -0.1 \\ 6 & 1 & 0 & 0 & 0 & 0 & 27.6 & 712.0 & 0.1 & -7.0 & 0.0 \\ 7 & 0 & 1 & 2 & -2 & 2 & 121.7 & -517.0 & 1.2 & 224.0 & -0.6 \\ 8 & 0 & 0 & 2 & 0 & 1 & 13.6 & -386.0 & -0.4 & 200.0 & 0.0 \\ 9 & 1 & 0 & 2 & 0 & 2 & 9.1 & -301.0 & 0.0 & 129.0 & -0.1 \\ 10 & 0 & -1 & 2 & -2 & 2 & 365.2 & 217.0 & -0.5 & -95.0 & 0.3 \\ 11 & -1 & 0 & 0 & 2 & 0 & 31.8 & 158.0 & 0.0 & -1.0 & 0.0 \\ 12 & 0 & 0 & 2 & -2 & 1 & 177.8 & 129.0 & 0.1 & -70.0 & 0.0 \\ 13 & -1 & 0 & 2 & 0 & 2 & 27.1 & 123.0 & 0.0 & -53.0 & 0.0 \\ 14 & 1 & 0 & 0 & 0 & 1 & 27.7 & 63.0 & 0.1 & -33.0 & 0.0 \\ 15 & 0 & 0 & 0 & 2 & 0 & 14.8 & 63.0 & 0.0 & -2.0 & 0.0 \\ 16 & -1 & 0 & 2 & 2 & 2 & 9.6 & -59.0 & 0.0 & 26.0 & 0.0 \\ 17 & -1 & 0 & 0 & 0 & 1 & -27.4 & -58.0 & -0.1 & 32.0 & 0.0 \\ 18 & 1 & 0 & 2 & 0 & 1 & 9.1 & -51.0 & 0.0 & 27.0 & 0.0 \\ 19 & -2 & 0 & 0 & 2 & 0 & -205.9 & -48.0 & 0.0 & 1.0 & 0.0 \\ 20 & -2 & 0 & 2 & 0 & 1 & 1305.5 & 46.0 & 0.0 & -24.0 & 0.0 \\ 21 & 0 & 0 & 2 & 2 & 2 & 7.1 & -38.0 & 0.0 & 16.0 & 0.0 \\ 22 & 2 & 0 & 2 & 0 & 2 & 6.9 & -31.0 & 0.0 & 13.0 & 0.0 \\ 23 & 2 & 0 & 0 & 0 & 0 & 13.8 & 29.0 & 0.0 & -1.0 & 0.0 \\ 24 & 1 & 0 & 2 & -2 & 2 & 23.9 & 29.0 & 0.0 & -12.0 & 0.0 \\ 25 & 0 & 0 & 2 & 0 & 0 & 13.6 & 26.0 & 0.0 & -1.0 & 0.0 \\ 26 & 0 & 0 & 2 & -2 & 0 & 173.3 & -22.0 & 0.0 & 0.0 & 0.0 \\ 27 & -1 & 0 & 2 & 0 & 1 & 27.0 & 21.0 & 0.0 & -10.0 & 0.0 \\ 28 & 0 & 2 & 0 & 0 & 0 & 182.6 & 17.0 & -0.1 & 0.0 & 0.0 \\ 29 & 0 & 2 & 2 & -2 & 2 & 91.3 & -16.0 & 0.1 & 7.0 & 0.0 \\ 30 & -1 & 0 & 0 & 2 & 1 & 32.0 & 16.0 & 0.0 & -8.0 & 0.0 \\ 31 & 0 & 1 & 0 & 0 & 1 & 386.0 & -15.0 & 0.0 & 9.0 & 0.0 \\ 32 & 1 & 0 & 0 & -2 & 1 & -31.7 & -13.0 & 0.0 & 7.0 & 0.0 \\ 33 & 0 & -1 & 0 & 0 & 1 & -346.6 & -12.0 & 0.0 & 6.0 & 0.0 \\ 34 & 2 & 0 & -2 & 0 & 0 & -1095.2 & 11.0 & 0.0 & 0.0 & 0.0 \\ 35 & -1 & 0 & 2 & 2 & 1 & 9.5 & -10.0 & 0.0 & 5.0 & 0.0 \\ 36 & 1 & 0 & 2 & 2 & 2 & 5.6 & -8.0 & 0.0 & 3.0 & 0.0 \\ 37 & 0 & -1 & 2 & 0 & 2 & 14.2 & -7.0 & 0.0 & 3.0 & 0.0 \\ 38 & 0 & 0 & 2 & 2 & 1 & 7.1 & -7.0 & 0.0 & 3.0 & 0.0 \\ 39 & 1 & 1 & 0 & -2 & 0 & -34.8 & -7.0 & 0.0 & 0.0 & 0.0 \\ 40 & 0 & 1 & 2 & 0 & 2 & 13.2 & 7.0 & 0.0 & -3.0 & 0.0 \\ 41 & -2 & 0 & 0 & 2 & 1 & -199.8 & -6.0 & 0.0 & 3.0 & 0.0 \\ 42 & 0 & 0 & 0 & 2 & 1 & 14.8 & -6.0 & 0.0 & 3.0 & 0.0 \\ 43 & 2 & 0 & 2 & -2 & 2 & 12.8 & 6.0 & 0.0 & -3.0 & 0.0 \\ 44 & 1 & 0 & 0 & 2 & 0 & 9.6 & 6.0 & 0.0 & 0.0 & 0.0 \\ 45 & 1 & 0 & 2 & -2 & 1 & 23.9 & 6.0 & 0.0 & -3.0 & 0.0 \\ 46 & 0 & 0 & 0 & -2 & 1 & -14.7 & -5.0 & 0.0 & 3.0 & 0.0 \\ 47 & 0 & -1 & 2 & -2 & 1 & 346.6 & -5.0 & 0.0 & 3.0 & 0.0 \\ 48 & 2 & 0 & 2 & 0 & 1 & 6.9 & -5.0 & 0.0 & 3.0 & 0.0 \\ 49 & 1 & -1 & 0 & 0 & 0 & 29.8 & 5.0 & 0.0 & 0.0 & 0.0 \\ 50 & 1 & 0 & 0 & -1 & 0 & 411.8 & -4.0 & 0.0 & 0.0 & 0.0 \\ 51 & 0 & 0 & 0 & 1 & 0 & 29.5 & -4.0 & 0.0 & 0.0 & 0.0 \\ 52 & 0 & 1 & 0 & -2 & 0 & -15.4 & -4.0 & 0.0 & 0.0 & 0.0 \\ 53 & 1 & 0 & -2 & 0 & 0 & -26.9 & 4.0 & 0.0 & 0.0 & 0.0 \\ 54 & 2 & 0 & 0 & -2 & 1 & 212.3 & 4.0 & 0.0 & -2.0 & 0.0 \\ 55 & 0 & 1 & 2 & -2 & 1 & 119.6 & 4.0 & 0.0 & -2.0 & 0.0 \\ 56 & 1 & 1 & 0 & 0 & 0 & 25.6 & -3.0 & 0.0 & 0.0 & 0.0 \\ 57 & 1 & -1 & 0 & -1 & 0 & -3232.9 & -3.0 & 0.0 & 0.0 & 0.0 \\ 58 & -1 & -1 & 2 & 2 & 2 & 9.8 & -3.0 & 0.0 & 1.0 & 0.0 \\ 59 & 0 & -1 & 2 & 2 & 2 & 7.2 & -3.0 & 0.0 & 1.0 & 0.0 \\ 60 & 1 & -1 & 2 & 0 & 2 & 9.4 & -3.0 & 0.0 & 1.0 & 0.0 \\ 61 & 3 & 0 & 2 & 0 & 2 & 5.5 & -3.0 & 0.0 & 1.0 & 0.0 \\ 62 & -2 & 0 & 2 & 0 & 2 & 1615.7 & -3.0 & 0.0 & 1.0 & 0.0 \\ 63 & 1 & 0 & 2 & 0 & 0 & 9.1 & 3.0 & 0.0 & 0.0 & 0.0 \\ 64 & -1 & 0 & 2 & 4 & 2 & 5.8 & -2.0 & 0.0 & 1.0 & 0.0 \\ 65 & 1 & 0 & 0 & 0 & 2 & 27.8 & -2.0 & 0.0 & 1.0 & 0.0 \\ 66 & -1 & 0 & 2 & -2 & 1 & -32.6 & -2.0 & 0.0 & 1.0 & 0.0 \\ 67 & 0 & -2 & 2 & -2 & 1 & 6786.3 & -2.0 & 0.0 & 1.0 & 0.0 \\ 68 & -2 & 0 & 0 & 0 & 1 & -13.7 & -2.0 & 0.0 & 1.0 & 0.0 \\ 69 & 2 & 0 & 0 & 0 & 1 & 13.8 & 2.0 & 0.0 & -1.0 & 0.0 \\ 70 & 3 & 0 & 0 & 0 & 0 & 9.2 & 2.0 & 0.0 & 0.0 & 0.0 \\ 71 & 1 & 1 & 2 & 0 & 2 & 8.9 & 2.0 & 0.0 & -1.0 & 0.0 \\ 72 & 0 & 0 & 2 & 1 & 2 & 9.3 & 2.0 & 0.0 & -1.0 & 0.0 \\ 73 & 1 & 0 & 0 & 2 & 1 & 9.6 & -1.0 & 0.0 & 0.0 & 0.0 \\ 74 & 1 & 0 & 2 & 2 & 1 & 5.6 & -1.0 & 0.0 & 1.0 & 0.0 \\ 75 & 1 & 1 & 0 & -2 & 1 & -34.7 & -1.0 & 0.0 & 0.0 & 0.0 \\ 76 & 0 & 1 & 0 & 2 & 0 & 14.2 & -1.0 & 0.0 & 0.0 & 0.0 \\ 77 & 0 & 1 & 2 & -2 & 0 & 117.5 & -1.0 & 0.0 & 0.0 & 0.0 \\ 78 & 0 & 1 & -2 & 2 & 0 & -329.8 & -1.0 & 0.0 & 0.0 & 0.0 \\ 79 & 1 & 0 & -2 & 2 & 0 & 23.8 & -1.0 & 0.0 & 0.0 & 0.0 \\ 80 & 1 & 0 & -2 & -2 & 0 & -9.5 & -1.0 & 0.0 & 0.0 & 0.0 \\ 81 & 1 & 0 & 2 & -2 & 0 & 32.8 & -1.0 & 0.0 & 0.0 & 0.0 \\ 82 & 1 & 0 & 0 & -4 & 0 & -10.1 & -1.0 & 0.0 & 0.0 & 0.0 \\ 83 & 2 & 0 & 0 & -4 & 0 & -15.9 & -1.0 & 0.0 & 0.0 & 0.0 \\ 84 & 0 & 0 & 2 & 4 & 2 & 4.8 & -1.0 & 0.0 & 0.0 & 0.0 \\ 85 & 0 & 0 & 2 & -1 & 2 & 25.4 & -1.0 & 0.0 & 0.0 & 0.0 \\ 86 & -2 & 0 & 2 & 4 & 2 & 7.3 & -1.0 & 0.0 & 1.0 & 0.0 \\ 87 & 2 & 0 & 2 & 2 & 2 & 4.7 & -1.0 & 0.0 & 0.0 & 0.0 \\ 88 & 0 & -1 & 2 & 0 & 1 & 14.2 & -1.0 & 0.0 & 0.0 & 0.0 \\ 89 & 0 & 0 & -2 & 0 & 1 & -13.6 & -1.0 & 0.0 & 0.0 & 0.0 \\ 90 & 0 & 0 & 4 & -2 & 2 & 12.7 & 1.0 & 0.0 & 0.0 & 0.0 \\ 91 & 0 & 1 & 0 & 0 & 2 & 409.2 & 1.0 & 0.0 & 0.0 & 0.0 \\ 92 & 1 & 1 & 2 & -2 & 2 & 22.5 & 1.0 & 0.0 & -1.0 & 0.0 \\ 93 & 3 & 0 & 2 & -2 & 2 & 8.7 & 1.0 & 0.0 & 0.0 & 0.0 \\ 94 & -2 & 0 & 2 & 2 & 2 & 14.6 & 1.0 & 0.0 & -1.0 & 0.0 \\ 95 & -1 & 0 & 0 & 0 & 2 & -27.3 & 1.0 & 0.0 & -1.0 & 0.0 \\ 96 & 0 & 0 & -2 & 2 & 1 & -169.0 & 1.0 & 0.0 & 0.0 & 0.0 \\ 97 & 0 & 1 & 2 & 0 & 1 & 13.1 & 1.0 & 0.0 & 0.0 & 0.0 \\ 98 & -1 & 0 & 4 & 0 & 2 & 9.1 & 1.0 & 0.0 & 0.0 & 0.0 \\ 99 & 2 & 1 & 0 & -2 & 0 & 131.7 & 1.0 & 0.0 & 0.0 & 0.0 \\ 100 & 2 & 0 & 0 & 2 & 0 & 7.1 & 1.0 & 0.0 & 0.0 & 0.0 \\ 101 & 2 & 0 & 2 & -2 & 1 & 12.8 & 1.0 & 0.0 & -1.0 & 0.0 \\ 102 & 2 & 0 & -2 & 0 & 1 & -943.2 & 1.0 & 0.0 & 0.0 & 0.0 \\ 103 & 1 & -1 & 0 & -2 & 0 & -29.3 & 1.0 & 0.0 & 0.0 & 0.0 \\ 104 & -1 & 0 & 0 & 1 & 1 & -388.3 & 1.0 & 0.0 & 0.0 & 0.0 \\ 105 & -1 & -1 & 0 & 2 & 1 & 35.0 & 1.0 & 0.0 & 0.0 & 0.0 \\ 106 & 0 & 1 & 0 & 1 & 0 & 27.3 & 1.0 & 0.0 & 0.0 & 0.0 \\\hline \end{array} }[/math]
- Table 2: IAU1980 Theory of Nutation model (http://hpiers.obspm.fr/eop-pc/models/nutations/nut_IAU1980.dat).
Notes
- ^ IAU Resolution B16 recommends that beginning on 1 January 2003 the IAU 1976 Precession Model and IAU 1980 Theory of Nutation be replaced by the IAU 2000 models. Equations, parameters, procedures and software routines implementing the IAU 2000 model can be found at the ftp://maia.usno.navy.mil/conv2003/chapter5/ (IERS Recommendations 2003).
References
- ^ [Yoder et al., 1981] Yoder, C., Williams, J. and Parke, M., 1981. Tidal Variations of Earth Rotation. Journal of Geophysical Research. pp. 881-891.