If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Frequency Lock Loop (FLL)
| Receivers | |
|---|---|
| Title | Frequency Lock Loop (FLL) |
| Edited by | GMV |
| Level | Advanced |
| Year of Publication | 2011 |
Frequency Lock Loops are part of the receiver's signal tracking loops, and aim at tracking the frequency of the incoming GNSS signal. The FLL provides frequency corrections in a continuous loop, generating a frequency error signal.
Principle
Frequency Lock Loops (FLL) track the Doppler frequency of the incoming signal (with respect to Intermediate Frequency), without necessarily correcting for phase. For that purpose, the FLL uses integrations, filters and Numerical Control Oscillators (NCO) – described here – as any other typical loop. In this case, the specificity relies on the discriminator used to assess the current frequency error estimated at the receiver.
The principle behind most common FLL implementation is to retrieve frequency information, by using the derivative of the phase between two consecutive sets of data (samples). As such, the common FLL is a differential-phase tracking loop. The FLL is expected to work well if the coherent integration time [math]\displaystyle{ T\, }[/math] is small, in order to avoid aliasing:
[math]\displaystyle{ \frac{-1}{2T}\lt \hat {f}\lt \frac{1}{2T}\, }[/math]
Other tracking strategies exist which operate on a different principles, for example, they may directly observe the frequency information via a DFT, or by observing the relative power in correlator values which are computed at various frequency offsets. [1]
Discriminators
First, let us define cross product and dot product, in terms of In-Phase I and Quadrature Q components, as:
[math]\displaystyle{ cross=I_{P1} \times Q_{P2} - I_{P2} \times Q_{P1}\, }[/math]
[math]\displaystyle{ dot=I_{P1} \times I_{P2} + Q_{P1} \times Q_{P2}\, }[/math]
where the indices 1 and 2 refer to samples taken at consecutive time instants, [math]\displaystyle{ t_1\, }[/math] and [math]\displaystyle{ t_2\, }[/math].
This way, the most commonly used FLL discriminators are (ordered from lowest to highest computational burden)[2]:
- [math]\displaystyle{ \frac{cross}{t_2-t_1}\, }[/math]
- [math]\displaystyle{ \frac{cross \times sign(dot)}{t_2-t_1}\, }[/math]
- [math]\displaystyle{ \frac{atan2 (cross, dot)}{t_2-t_1}\, }[/math]
The [math]\displaystyle{ atan2\, }[/math] discriminator is optimal, although it presents the greatest computational requirements. Note that the FLL is insensitive to data transitions, as long as the consecutive measurements (correlator outputs) refer to the same data bit.
Performance
The main sources of errors in the FLL are frequency jitter and dynamic stress error[2], which are mostly caused by thermal noise. The FLL thermal noise jitter can be written (in m/s) as:
[math]\displaystyle{ \sigma_{th}=\frac{\lambda}{2 \pi T} \sqrt{\frac{4FB_n}{C/N_0}(1+\frac{1}{TC/N_0})}\, }[/math]
where:
- [math]\displaystyle{ \lambda\, }[/math] is the wavelength of the carrier signal [m].
- [math]\displaystyle{ B_n\, }[/math] is the loop bandwidth [Hz].
- [math]\displaystyle{ C/N_0\, }[/math] is the carrier-to-noise ratio [dB-Hz].
- [math]\displaystyle{ T\, }[/math] is the integration time [s].
- [math]\displaystyle{ F\, }[/math] = 1, at high carrier to noise ration; [math]\displaystyle{ F\, }[/math] = 2, otherwise.
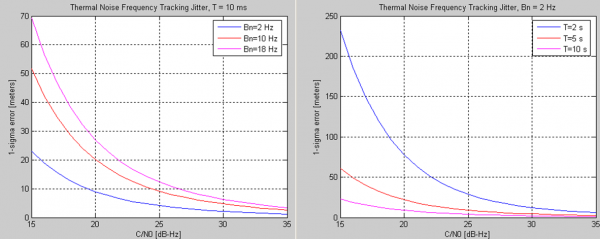
The performance of the FLL depends mainly on the loop bandwidth and the integration times used to accumulate the correlator outputs. The impact of these parameters is shown in Figure 1, and they are visible mainly for low carrier to noise ratio.
These results also illustrate the fact that longer integration times (and lower bandwidths) lead to noise reduction, hence higher performances, as discussed here. In addition, lower loop noise bandwidths allow coping with higher dynamic environments.
Related articles
- Generic Receiver Description
- Baseband Processing
- Digital Signal Processing
- Tracking Loops
- Phase Lock Loop (PLL)
- Delay Lock Loop (DLL)