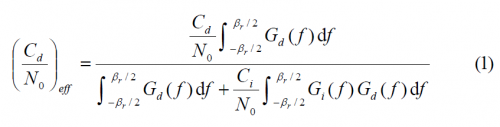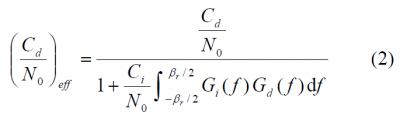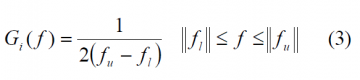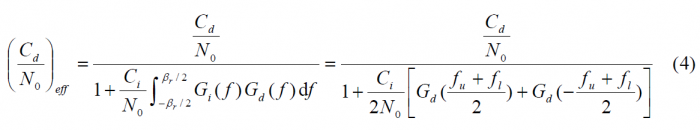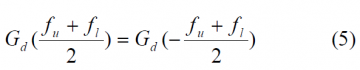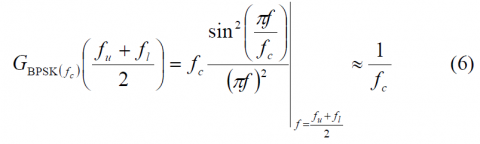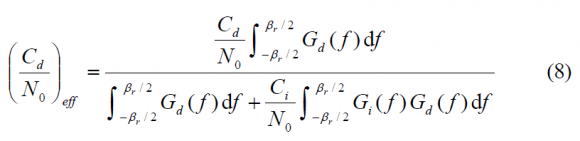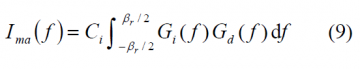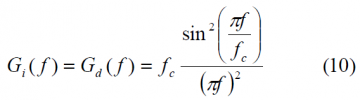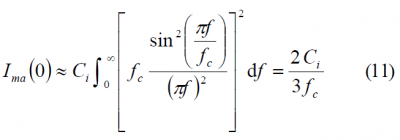If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Equivalent Carrier to Noise Ratio in presence of RF interference
| Fundamentals | |
|---|---|
| Title | Equivalent Carrier to Noise Ratio in presence of RF interference |
| Author(s) | J.A Ávila Rodríguez, University FAF Munich, Germany. |
| Level | Advanced |
| Year of Publication | 2011 |
This article derives some expressions of interest for the Equivalent Carrier to Noise Ratio in presence of RF interference. As we know, one of the main effects of RF interference is to reduce the [math]\displaystyle{ C_d/N_0 }[/math] of the desired signal d, as shown next:
where the subindex i refers to the interfering signal and d to the desired signal. We can further simplify this expression if we assume that all the power of the desired satellite fits into the bandwidth of the receiver, simplifying the effective [math]\displaystyle{ C_d/N_0 }[/math] to:
We can classify RF interference sources into narrowband interference and wideband interference. For the case of narrowband interference, the power spectral density of the interfering signal can be approximated as rectangular, such that:
Furthermore, if we assume that the whole interfering narrowband signal is in-band, then the effective [math]\displaystyle{ C_d/N_0 }[/math] will be:
In addition, since the Power Spectral Density is even,
and assuming that the narrowband interference has a low frequency relative to the chip rate, we can use the following approximation for the particular case of BPSK[math]\displaystyle{ \left ( f_c \right ) }[/math]:
Finally, as shown in [P. Ward, 1994][1], the effective [math]\displaystyle{ C_d/N_0 }[/math] will be for the case of a narrowband interferer:
On the other hand, for the case of a wideband interferer, the expression to apply is the following:
where we can recognize the spectral separation coefficient (SSC) in the denominator. In fact, the lower the value the SSC adopts, the more robust will be the signal against wideband and narrowband interferers as shown in the expressions above.
Using again the example of a BPSK signal, the multiple access interference will adopt the following form:
where for the particular case of the intra-system interference or for the case of an interferer matching the spectrum of the desired signal, BPSK in our example, we have:
As we can recognize, this term appears in the denominator of (8). Moreover, if we assume a large processing gain, the multiple access interference will only be significant around zero simplifying the interference to the following [J.J. Spilker, 1997] [2]:
As we expected, if we express now [math]\displaystyle{ 2/3 f_c }[/math] in dB for a chip rate of 1.023 MHz, we obtain the figure of -61.8597 for the C/A Code Self SSC.
References
- ^ [P. Ward, 1994] P. Ward, Dual Use of Military Anti-Jam GPS Receiver Design Techniques for Commercial Aviation RF Interference Integrity Monitoring, Proceedings of the US Institute of Navigation ION-AM 1994.
- ^ [J.J. Spilker, 1997] J.J. Spilker, GPS Signal Structure and Theoretical Performance in Global Positioning System: Theory and Applications Volume I, Progress in Astronautics and Aeronautics Volume 164, AIAA, pp. 57-120.
Credits
The information presented in this NAVIPEDIA’s article is an extract of the PhD work performed by Dr. Jose Ángel Ávila Rodríguez in the FAF University of Munich as part of his Doctoral Thesis “On Generalized Signal Waveforms for Satellite Navigation” presented in June 2008, Munich (Germany)