If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
APPROVED
Not Approved
Vicente.Navarro approved this page 25 September 2025
25 September 2025
Clock Modelling
Jump to navigation
Jump to search
| Fundamentals | |
|---|---|
| Title | Clock Modelling |
| Author(s) | J. Sanz Subirana, J.M. Juan Zornoza and M. Hernández-Pajares, Technical University of Catalonia, Spain. |
| Level | Intermediate |
| Year of Publication | 2011 |
The clock offsets are due to clock synchronism errors referring to GNSS (GPS, GLONASS, Galileo...) time scale. The modelling of such offsets, as well as its effect on the navigation solution, is described as follows.
- Receiver clock offset([math]\displaystyle{ \delta t_{rcv} }[/math]): It is estimated together with the receiver coordinates, thence no modelling is needed in this case.
- Satellite clock offset ([math]\displaystyle{ \delta t^{sat} }[/math]): It can be split in two terms [footnotes 1]:
- [math]\displaystyle{ \delta t^{sat}=\tilde{\delta t}^{sat}+\Delta_{rel} \qquad \mbox{(1)} }[/math]
- The first term ([math]\displaystyle{ \tilde{\delta t}^{sat} }[/math]) can be calculated from values broadcasted in the navigation messages (for the Standard Point Positioning) or from the precise products available from IGS centres or other providers (see Precise Point Positioning) The second term [math]\displaystyle{ \Delta_{rel} }[/math] is small relativistic correction caused by the orbital eccentricity, see equation (2) in Relativistic Clock Correction.
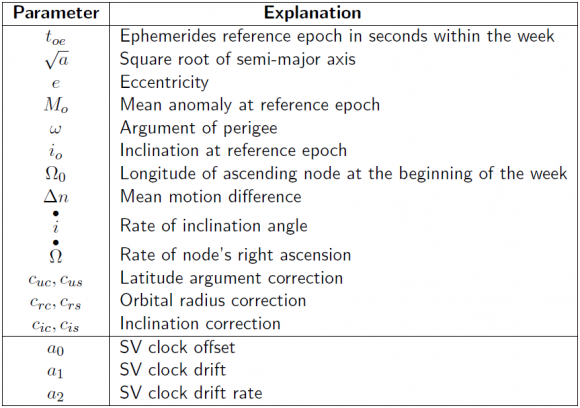
- The broadcast navigation message provides the clock information as the coefficients of a polynomial, in a given reference epoch ([math]\displaystyle{ t_0 }[/math]) to compute the satellite clock offset as:
- [math]\displaystyle{ \tilde{ \delta t}^{sat}=a_0+a_1(t-t_0)+a_2(t-t_0)^2 \qquad \mbox{(2)} }[/math]
- In GLONASS, as the message is updated every 1/2h, only a first order polynomial is considered, being ([math]\displaystyle{ a_0=-\tau_n }[/math]) the clock offset and ([math]\displaystyle{ a_1=\gamma_n }[/math]) the relative frequency offset, see table 2. Note that in the RINEX files the [math]\displaystyle{ -\tau_n }[/math] value is given instead of [math]\displaystyle{ \tau_n }[/math].
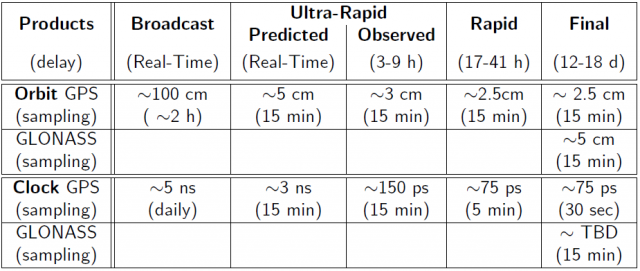
- The accuracy of broadcasted clocks is at the order of some nanoseconds [footnotes 2].
- The precise GPS and GLONASS satellite clocks provided by IGS are accurate at the order of [math]\displaystyle{ 0.1 }[/math] nanosecond or better [footnotes 3], see table 3.
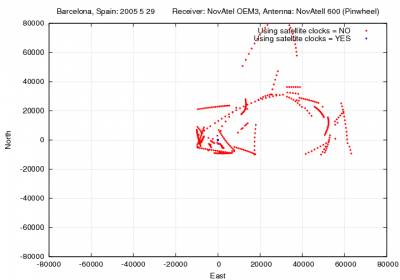
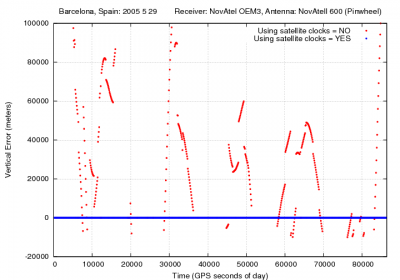
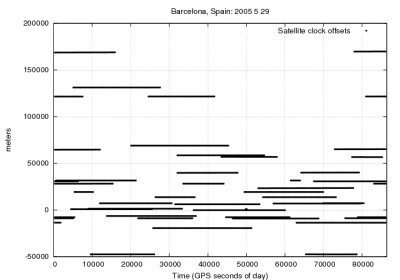
- Figure 1 illustrates the effect of neglecting the GPS satellite clock offsets on the user position. As it is shown the satellite clocks reach up to more than [math]\displaystyle{ 150 }[/math] kilometres, which leads to huge position errors.
Figure 1: Satellite clocks: Range and position domain effect First row shows the horizontal (left) and vertical (right) positioning error using (blue) or not using (red) the satellite clock offsets. The variation in range is shown in the second row at left.
For further information see Relativistic Clock Correction.
Notes
- ^ GLONASS satellites transmit the [math]\displaystyle{ \Delta_{rel} }[/math] within the satellite clock corrections [math]\displaystyle{ \tilde{\delta t}^{sat} }[/math].
- ^ With the GPS Selective availability activated they can be degraded up to more than [math]\displaystyle{ 100 }[/math] nanoseconds.
- ^ Notice that [math]\displaystyle{ 1 }[/math] nanosecond of error means [math]\displaystyle{ 30 }[/math] centimetres in range.