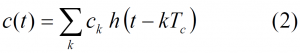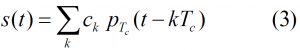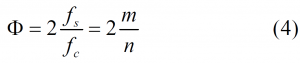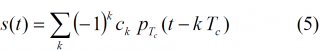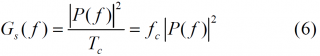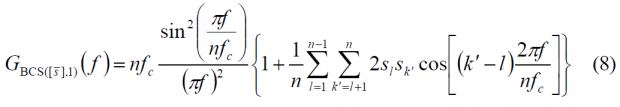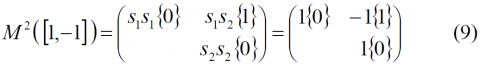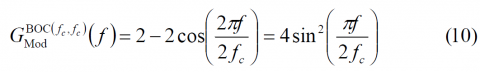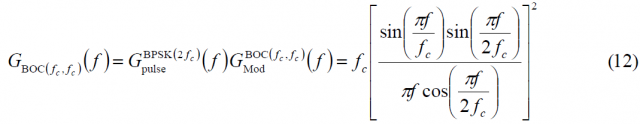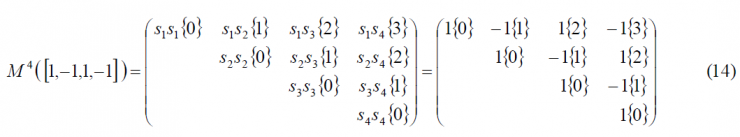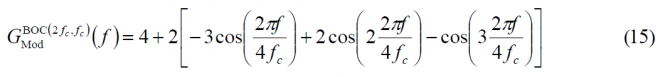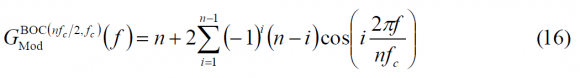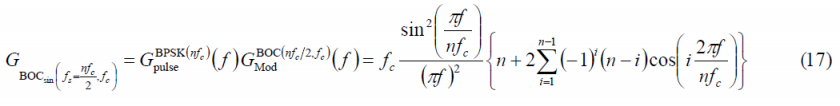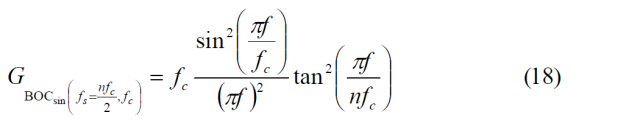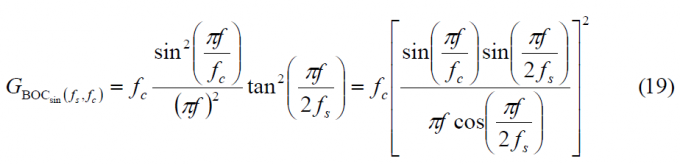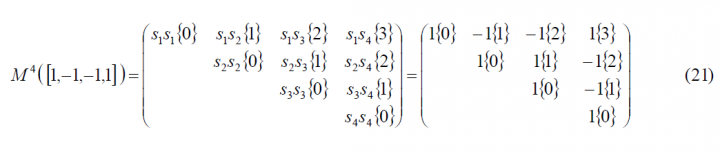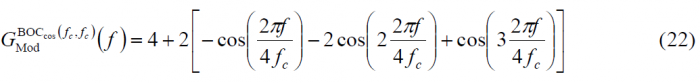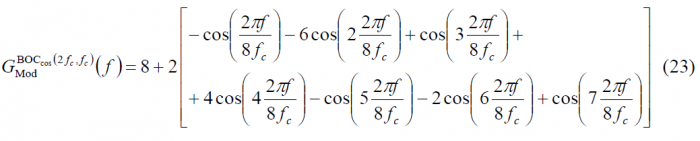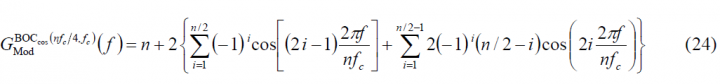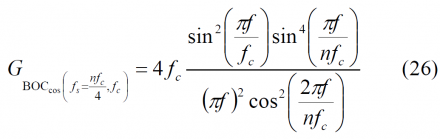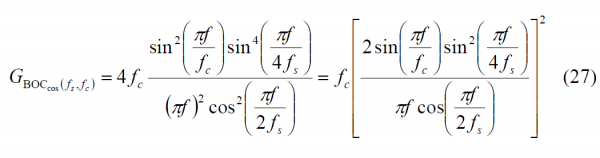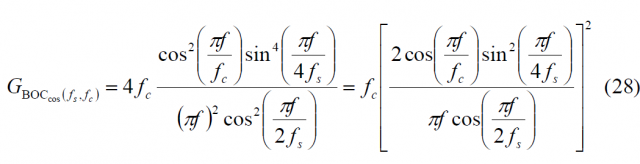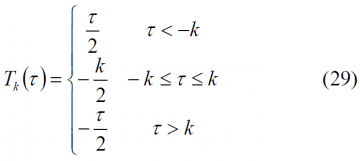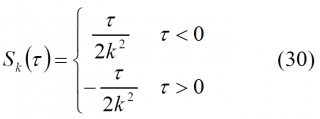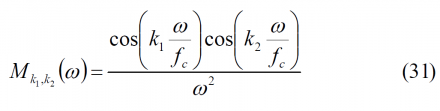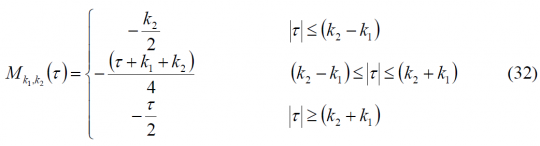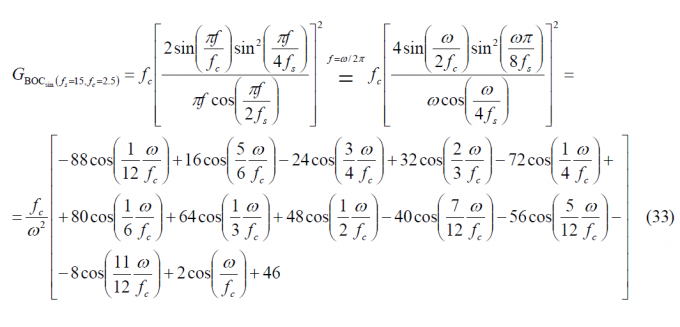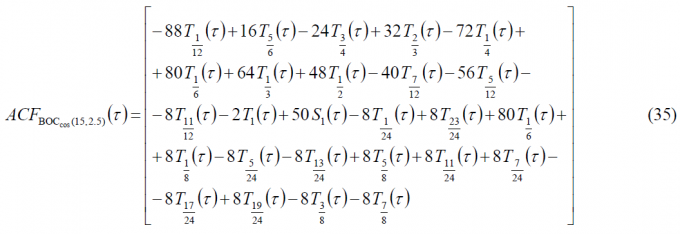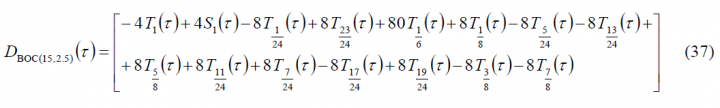If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Binary Offset Carrier (BOC)
| Fundamentals | |
|---|---|
| Title | Binary Offset Carrier (BOC) |
| Author(s) | J.A Ávila Rodríguez, University FAF Munich, Germany. |
| Level | Advanced |
| Year of Publication | 2011 |
Binary Offset Carrier Signals are a particular case of BCS signals with a representation vector formed by +1’s and -1’s alternating in a particular defined way. Two notations [E. Rebeyrol et al., 2005] [1] can be found in the literature to define the BOC signals. We describe them shortly in the following lines.
The first model defines the BOC modulation as the result of multiplying the PRN code with a sub-carrier which is equal to the sign of a sine or a cosine waveform, yielding so-called sine-phased or cosine-phased BOC signals respectively as shown in [J.W. Betz, 2001] [2], [L.R.Weill, 2003] [3], [J. Godet, 2001] [4] and [E. Rebeyrol et al., 2005] [1]. According to this definition, the expression of the sine-phased BOC signal would be:
- with
where
- [math]\displaystyle{ c_k }[/math] is the code sequence waveform,
- [math]\displaystyle{ f_s }[/math] is the sub-carrier frequency,
- and [math]\displaystyle{ h\left(t\right) }[/math] is the Non Return to Zero (NRZ) code materialization with value 1 over the support [math]\displaystyle{ \left [ 0, T_c \right ) }[/math].
The second model defines the BOC modulation as follows:
where [math]\displaystyle{ p_{T_e}\left(t\right) }[/math] describes the chip waveform and is broken up into n rectangular pulses of duration [math]\displaystyle{ T_c / n }[/math] with amplitude ±1. It is important to note that in this case the sine-phasing or cosine-phasing is considered as part of the chip waveform definition. This convention has been introduced in [A.R. Pratt and J.I.R. Owen, 2003a] [5] and [J.W. Betz, 2001][2].
No matter what definition we choose to describe the BOC modulation in the time domain, the BOC signal is commonly referred to as BOC(fs, fc) where [math]\displaystyle{ f_s = m \cdot 1.023 }[/math] and [math]\displaystyle{ f_c = n \cdot 1.023 }[/math] so that generally one only says BOC(m, n) for simplicity. Moreover, unless it is indicated in a different way, when we talk about BOC signals we will always mean the sine-phased variant.
The parameter [math]\displaystyle{ \Phi }[/math] is of great interest when analysing BOC signals. It is defined as two times the ratio between the sub-carrier and the chip frequency as follows:
As we can see, [math]\displaystyle{ \Phi }[/math] represents the number of half periods of the sub-carrier that fit in a code chip so that this ratio can be even or odd. When [math]\displaystyle{ \Phi }[/math] is even, the two definitions presented above for the BOC modulation coincide since we can consider the sub-carrier as included in the chip waveform. However, when [math]\displaystyle{ \Phi }[/math] is odd the second definition is not valid any more. The following example shows this. Indeed, depending on the convention that we adopt to define the BOC signal we can see that different time series result.
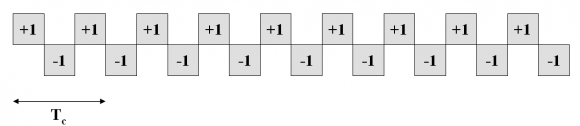
Consider the code sequence {1,-1,1, -1,1,1} and a sine-phased waveform with [math]\displaystyle{ 2 f_s / f_c = 3 }[/math]. If we employ the first convention, the rectangular sub-carrier that results from taking the sign of the sine waveform will be as follows:
Accordingly, the product of the binary sub-carrier (1) with the code sequence results in the following time series:
where all the transitions have been underlined in red. If we follow now the approach of defining the sub-carrier as part of the chip waveform as it is done in the second definition, the chip waveform to use will be:
and the resulting time series will be as follows:
If we compare now Figure 2 and Figure 4 we can clearly recognize that the two definitions of BOC do not lead to an unique time series representation. Indeed the difference is a polarity inversion every two bits as identified in [E. Rebeyrol et al., 2005] [1].
We conclude thus that if [math]\displaystyle{ \Phi }[/math] is odd, a slight modification must be made in the second definition to account for the effect of the sub-carrier onto the code as shown in [J.W. Betz, 2001] [2]. Indeed, the new definition should be for the case of [math]\displaystyle{ \Phi }[/math] odd as follows:
resulting then both conventions in the same time series.
If we look at the equations above in detail, we can recognize the term [math]\displaystyle{ {\left ( -1 \right )}^k }[/math] introduced in the expression, what can be interpreted as a modification of the PRN sequence so that all the even code positions would alternate. Indeed, the new code would be then [math]\displaystyle{ {\left ( -1 \right )}^k c_k }[/math] instead of the original [math]\displaystyle{ c_k }[/math]. As a conclusion, in the case of [math]\displaystyle{ \Phi }[/math] odd a modification must be made on the code sequence if we want the sub-carrier to be included in the chip waveform. This does not represent a real problem from a theoretical point of view but it is important to note that depending on which convention is used, the receiver must be adapted consequently because otherwise it would suffer from non desired losses [E. Rebeyrol et al., 2005] [1].
Once the two definitions of BOC have been presented, it seems that the first one represents better the original definition of the BOC signal since no exception in the definition must be made depending on whether the figure [math]\displaystyle{ \Phi = 2 \frac {f_s}{f_c} }[/math] is even or odd. Nonetheless, the second convention allows for easier and more tractable derivations in some cases and thus both conventions will be indistinctively used.
Moreover, we have shown that the second convention is also correct as long as the PRN code is correspondingly modified. We will derive expressions for smooth spectra and assume consequently that the PRN code shows ideal properties. The modified code version should also present similar ideal properties and we can directly consider the sub-carrier as included in the code materialization. This will considerably simplify the derivations. Consequently we can use
to calculate the power spectral density of BOC. This is actually not only valid for the BOC modulation, but for all the signals that can be expressed as shown in
Last but not the least, it must be noted that for non-ideal codes or very short codes this is not true any more.
It is important to note that the conclusions derived above for the sine-phased BOC modulation can easily be extended to the cosine case and to any BCS signal in general. In fact, also for a BCS signal we can distinguish between even and odd BCS signals in a similar manner as we did above. However, the examples might not be so easy to analyse in this case.
Binary Offset Carrier with sine phasing: [math]\displaystyle{ BOC_{sin}\left ( f_s, f_c \right ) }[/math]
The Binary Offset Carrier Modulation can be expressed as a BCS sequence with a vector that is formed by alternating +1 and -1 a number of times [math]\displaystyle{ f_s / f_c }[/math]. In the next lines we will derive the general expression of the power spectral density.
To do so, we recall
and we build up the corresponding matrix to calculate [math]\displaystyle{ G_{Mod} \left ( f \right ) }[/math] as defined in Binary Coded Symbols (BCS) . As we will see next, the matrix shows symmetry properties that will allow to simplify the problem considerably.
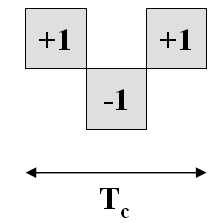
To start, let us analyse the particular case of [math]\displaystyle{ BOC \left ( f_s, f_c \right ) }[/math] As we saw in the preceding lines, [math]\displaystyle{ BOC \left ( f_c, f_c \right ) }[/math], also known as [math]\displaystyle{ BOC_{sin} \left ( f_c, f_c \right ) }[/math], can be expressed as BCS([1,-1], fc) and presents thus the following matrix:
According to this
adopting the pulse term of the PSD the following form:
Finally, according to (8), the power spectral density of this particular case would be:
Let us now extend this expression to any [math]\displaystyle{ BOC_{sin} \left ( f_s, f_c \right ) }[/math] generalizing on [math]\displaystyle{ f_s / f_c }[/math] with [math]\displaystyle{ f_s / f_c }[/math] being an integer, namely the number of times that the pair {1,-1} repeats. Indeed, once we have found the expression [math]\displaystyle{ G_{Mod} \left ( f \right ) }[/math] with [math]\displaystyle{ f_s / f_c = 1 }[/math], we calculate for [math]\displaystyle{ f_s / f_c = 2 }[/math] in the same manner:
where the definition matrix is shown to be:
and thus
It is interesting to note that the term in the brackets resembles a Fourier series until term n-1. If we continue now by induction we can see that the expression for any n adopts the following form:
Where [math]\displaystyle{ n \in \left \{ 2,4,6,8, \cdots \right \} }[/math]. It must be noted that the variable n refers to the number of subchips and not to the number of times that the sub-carrier contains the code rate as usually done in the literature. Once we have obtained the modulating term of the power spectral density, the general form of the PSD for any sine-phased BOC modulation can be expressed as:
which can be explicitly simplified as:
As a conclusion, the BOC signal in sine phase can be considered as a BCS signal whose sequence is formed by concatenating [+1,-1] a number of times [math]\displaystyle{ f_s / f_c }[/math]. Thus the length n will be [math]\displaystyle{ 2f_s / f_c }[/math] and (18) can also be expressed as:
which is the well known form we find in the literature [J.W. Betz, 2001] [2].
Binary Offset Carrier with cosine phasing: [math]\displaystyle{ BOC_{cos}\left ( f_s, f_c \right ) }[/math]
Following the same approach of the previous section, we will derive next the well-known expression for the power spectral density of the BOC modulation with sub-carrier in cosine phasing. Taking as an example the sine-phased BOC signal of the lines above, we will derive now also a general expression by induction over n. Let us begin with [math]\displaystyle{ BOC_{cos}\left ( f_c, f_c \right ) }[/math]:
The corresponding definition matrix under these assumptions is shown to be:
Thus, the modulating function adopts the following form:
If we repeat now the calculation for [math]\displaystyle{ BOC_{cos}\left ( 2f_c, f_c \right ) }[/math] in order to derive the generalized expression by induction over n, we have [math]\displaystyle{ BOC_{cos}\left ( f_s, f_c \right ) = BOC_{cos}\left ( 2f_c, f_c \right ) }[/math] or [math]\displaystyle{ BCS \left ( \left [1,-1,-1,1,1,-1,-1,1 \right] , f_c \right) }[/math], so that
If we generalize now, we can see that the expression for any n will adopt the following form:
Where [math]\displaystyle{ n \in \left \{4,8,12,16,\cdots \right \} }[/math]. Finally, once we have obtained the modulating term of the power spectral density for any n, we can express the power spectral density of any cosine-phase BOC signal as follows:
After some math (25) can still be explicitly expressed for the even case as follows:
The BOC signal in cosine phase can be considered as a BCS signal whose sequence is formed by concatenating [1,-1,-1,1] a number of times [math]\displaystyle{ f_s / f_c }[/math]. Thus the length n will be [math]\displaystyle{ 4f_s / f_c }[/math] and (26) simplifies to:
In the same manner, for the odd case cosine-phase we have:
Autocorrelation function of a generic BOC signal
One of the most interesting figures in the analysis of the signal structure is the autocorrelation function of the chip waveform as we saw at the beginning of this chapter. In this chapter we will derive general expressions to define the analytical shape of the autocorrelation function a generic BOC signal with infinite bandwidth. This will help us understand the importance of having a good autocorrelation function in order to have good ranging potential for positioning. Additionally, analytical expressions will permit us establishing comparisons between sine- and cosine-phased BOC modulations and investigate the effect that extra terms in the definition of the ACF can bring. Before that, we derive first the inverse Fourier Transform of some functions of interest. The importance of these functions lies in the fact that since the Power Spectral Density of any MCS signal can be developed as a series with them, the derivation of analytical expressions for the ACF will be then possible no matter how complex the shape of the signal is.
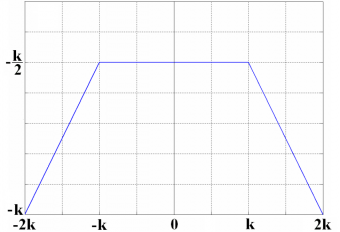
As we know, the inverse Fourier transform of [math]\displaystyle{ T_k \left ( \omega \right ) = cos \left ( k \omega / f_c \right ) / {\omega}^2 }[/math] can be defined as follows:
where k fixes the height of the function at [math]\displaystyle{ \tau = 0 }[/math]. Moreover, the function [math]\displaystyle{ T_k \left ( \tau \right ) }[/math] is expressed as a function of [math]\displaystyle{ \tau }[/math] [chips]. Next the trapezoid function is shown graphically:
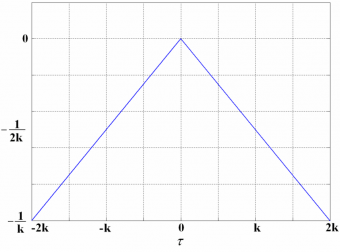
Also, the Fourier inverse Transform of [math]\displaystyle{ S_k \left( \omega \right ) = \frac{1}{ \left ( k \omega \right)^2} }[/math] can be expressed by means of a function that we will call [math]\displaystyle{ S_k \left ( \tau \right ) }[/math] as follows:
For the more general case, we will define the inverse Fourier Transform of
as:
where we assume that [math]\displaystyle{ k_2 \ge k_1 }[/math] without loss of generality. In addition, we can clearly see that [math]\displaystyle{ T_k \left ( \tau \right ) }[/math]is a particular case of [math]\displaystyle{ M_{k_1,k_2} \left ( \tau \right ) }[/math] since [math]\displaystyle{ M_{0,k_2} \left ( \tau \right ) = T_{k_2} \left ( \tau \right ) }[/math].
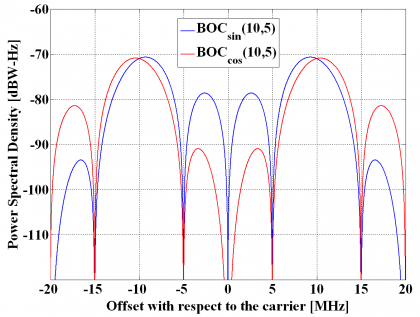
Next we compare the BOC signal in sine and cosine phasing for different chip rates. For exemplification we will take a sub-carrier rate of 10.23 MHz and a code rate of 5.115 MHz. We recall that these modulations correspond to the GPS M-Code and the Galileo PRS (E6).
The difference between the sine-phased and cosine-phased BOC modulation is even more obvious when we look at the [math]\displaystyle{ BOC_{sin}\left ( 15, 2.5 \right ) }[/math] and [math]\displaystyle{ BOC_{cos}\left ( 15, 2.5 \right ) }[/math] signals. As we can see, while the sine-phased concentrates more power at inner frequencies, so does the cosine version at outer frequencies.
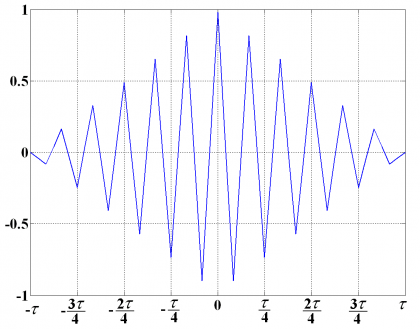
Now that we have the tools to derive the generic form of the ACF of any MCS signal, we develop the power spectral density of [math]\displaystyle{ BOC_{sin}\left ( 15, 2.5 \right ) }[/math] as follows:
And using the formulations derived in previous pages, we can express the ACF as follows:
which adopts graphically the following form:
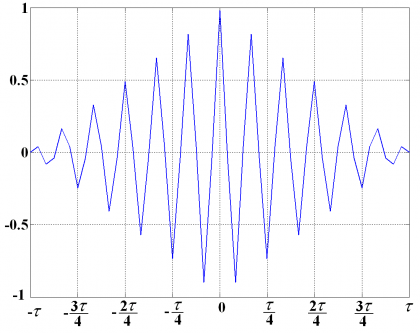
In the same manner, the power spectral density of [math]\displaystyle{ BOC_{cos}\left ( 15, 2.5 \right ) }[/math] can be equally expressed in terms of the functions defined above such that the ACF is shown to adopt the following form:
If we compare now (34) and (35) we see that we can express the ACF of the cosine-phase BOC as a function of the ACF of the sine-phased BOC in the following way:
where
what can be graphically shown as follows:
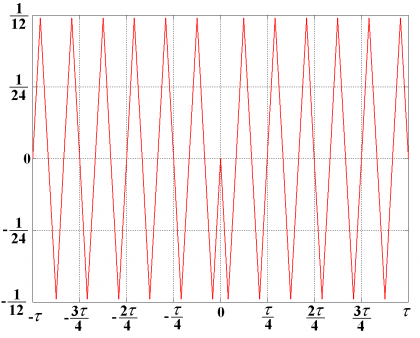
By looking at Figure 11 the following interesting properties can be observed:
- We can distinguish 6 peaks on every side with an amplitude of . In fact, for the general case we will have n peaks on every side with an amplitude where [math]\displaystyle{ n = f_s / f_c }[/math].
- This function shows the interesting property that we can easily convert the sine-phased autocorrelation function of any BOC signal into its cosine-phased counterpart by adding the corresponding difference function shown above.
Moreover, if we calculate now the Fourier transform of (37), we obtain the following spectrum:
As we can recognize, this spectrum is the difference between the power spectral densities of the sine-phased and cosine-phased BOC(15,2.5) modulations.
BOC signals vs. BPSK signals
The BOC modulation was the first attempt to modernize the GNSS signals and has indeed opened a new field of research in navigation that has recently lead to the AltBOC and MBOC solutions. These will be described in the following pages. As commented by [J.-A. Avila-Rodriguez et al., 2006d][6] and [G.W. Hein et al., 2006a][7], while very good performance can be obtained with the C/A code signal, it has been recognized that better performance can be obtained using spreading modulations that provide more power at high frequencies away from the centre frequency. In fact, this is the main idea behind the BOC modulation where a sub-carrier signal shifts spectral components to outer parts of the. The old BPSK modulation that is currently still used for GPS C/A code has limited capability for ranging and requires high performance receivers to use very wide front-end bandwidths as shown in [J. W. Betz and D. B. Goldstein, 2002][8]. Moreover, Intra-system interference is exacerbated by the short C/A codes. The relatively slow 1.023 MHz spreading code rate of the BPSK-R modulation offers limited channel capacity, restricting the number of simultaneous signals as well as the tolerable power differential between signals. Additionally, the data message modulated on the C/A code signal is inefficient and inflexible.
An interesting aspect of the BOC signal regarding its complexity is that it can be considered as two BPSKs shifted to [math]\displaystyle{ - f_s }[/math] and [math]\displaystyle{ + f_s }[/math] by the sub-carrier signal. Indeed many receiver implementations will make use of this principle to receive the future BOC signals. Side-lobe processing is thus a promising solution to treat BOC signals using the old BPSK architecture if we realize that a BOC signal is qualitatively similar to two BPSK signals with each half the power [J.W. Betz et al., 2005][9]. This idea is also of interest to process the AltBOC.
References
- ^ a b c d [E. Rebeyrol et al., 2005] E. Rebeyrol, C. Macabiau, L. Lestarquit, L. Ries, J-L. Issler, M.L. Boucheret, M. Bousquet , BOC Power Spectrum Densities, Proceedings of the National Technical Meeting of the Institute of Navigation, ION-NTM 2005, 24-26 January 2005, Long Beach, California, USA.
- ^ a b c d [J.W. Betz, 2001a] J.W. Betz, Binary Offset Carrier Modulations for Radionavigation, NAVIGATION: Journal of The Institute of Navigation Vol. 48, No. 4, Winter 2001/02.
- ^ [L.R.Weill, 2003] L. R. Weill, Multipath mitigation—how good can it get with new signals?” GPS World, vol. 16, no. 6, pp. 106–113, 2003.
- ^ [J. Godet, 2001] J. Godet, Technical Annex to Galileo SRD Signal Plans, STF annex SRD 2001/2003 Draft 1, July 2003.
- ^ [A.R. Pratt and J.I.R. Owen, 2003a] Anthony R. Pratt & John I.R. Owen, BOC Modulations Waveform, Proceedings of the International Technical Meeting of the Institute of Navigation, ION-GNSS 2003, 9-12 September 2003, Portland, Oregon, USA.
- ^ [J.-A. Avila-Rodriguez et al., 2006d] J.-A. Avila-Rodriguez, G. W. Hein, S. Wallner, A.R. Pratt, J.I.R. Owen, J.-L Issler, J.W. Betz, C.J. Hegarty, S. Lenahan, J.J. Rushanan, A.L. Kraay, T.A. Stansell, MBOC: The New Optimized Spreading Modulation Recommended for Galileo E1 OS and GPS L1C, ESA Navitec 2006, 11-13 December, 2006, Noordwijk, The Netherlands.
- ^ [G.W. Hein et al., 2006a] G. W. Hein, J.-A. Avila-Rodriguez, S. Wallner, A.R. Pratt, J.I.R. Owen, J.-L Issler, J.W. Betz, C.J. Hegarty, S. Lenahan, J.J. Rushanan, A.L. Kraay, T.A. Stansell, MBOC: The New Optimized Spreading Modulation Recommended for Galileo L1 OS and GPS L1C, Proceedings of the International Technical Meeting of the Institute of Navigation, IEEE/ION PLANS 2006, 24-27 April, 2006, Loews Coronado Bay Resort, San Diego, California, USA.
- ^ [J. W. Betz and D. B. Goldstein, 2002] J. W. Betz and D. B. Goldstein, Candidate designs for an additional civil signal in GPS spectral bands, Technical Papers, January 2002, MITRE, Bedford, Massachussets, USA.
- ^ [J.W. Betz et al., 2005] J.W. Betz, J.D. Fite, P.T. Capozza, Getting to M-Direct Acquisition of the New Military Signal, GPS World, April 2005, pp. 40-46.
Credits
The information presented in this NAVIPEDIA’s article is an extract of the PhD work performed by Dr. Jose Ángel Ávila Rodríguez in the FAF University of Munich as part of his Doctoral Thesis “On Generalized Signal Waveforms for Satellite Navigation” presented in June 2008, Munich (Germany)