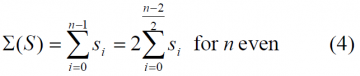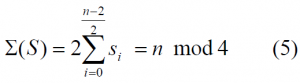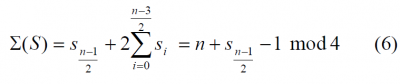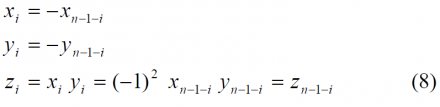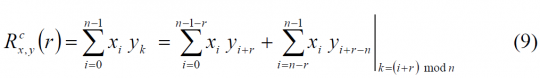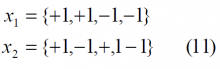If you wish to contribute or participate in the discussions about articles you are invited to contact the Editor
Antisymmetric Sequences
| Fundamentals | |
|---|---|
| Title | Antisymmetric Sequences |
| Author(s) | J.A. Ávila Rodríguez, University FAF Munich, Germany. |
| Level | Advanced |
| Year of Publication | 2011 |
MBOC is the result of multiplexing BOC(1,1) and BOC(6,1). In the long process of finding an alternative to BOC(1,1), experts of the Signal Task Force of the EC realized that some specific BCS sequences seemed to be of special interest for satellite navigation. CBCS presented the problem of having a tracking bias when correlated with a pure BOC(1,1) receiver, what lead to further investigations on alternative BCS sequences with particular symmetry properties. These receive the name of antisymmetric sequences and have been studied in [A.R. Pratt et al., 2006][1]. In the next lines the most important characteristics are underlined.
Let the binary sequence [math]\displaystyle{ S=\left \{s_i \right \} }[/math] of length n define a reversed sequence [math]\displaystyle{ S^* }[/math] such that:
It is important to note that this sequence can be any generic BCS signal in principle. A sequence is defined to be symmetric if [math]\displaystyle{ S^* = S }[/math], so that:
As we can see, such a definition allows solutions for both n even or odd. Furthermore, a binary sequence is defined as antisymmetric if [math]\displaystyle{ S^* = -S }[/math], that is:
As we can see, antisymmetric sequences may only be composed with even values of n, since there cannot be a central element, [math]\displaystyle{ x_{\left ( n-1 \right ) /2} }[/math] which is self inverse.
Another important characteristic of any generic BCS sequence is the balance. As shown in [A.R. Pratt et al., 2006] [1], the balance of a symmetric binary sequence can be determined through a consideration of the sum of the elements. Let [math]\displaystyle{ S= \left \{s_i \right \} }[/math] be a symmetric binary sequence of length n, then the sum [math]\displaystyle{ \sum \left ( S \right ) }[/math] of the element values is:
Moreover, assuming that the sequence is binary and n even, it can also be shown that
Equally, when n is odd, the sum of the elements of S adopts the following form:
As we can recognize, all antisymmetric binary sequences with even n are balanced because of their particular construction. Moreover as a consequence of (5), the sequence balance, that means [math]\displaystyle{ \sum \left ( S \right ) = 0 }[/math], can only be achieved for symmetric binary sequences whose lengths are multiples of 4. This is a necessary condition for the existence of some zero sum sequences, but not sufficient.
We further define the properties of a product sequence [math]\displaystyle{ Z=\left \{ z_i \right \} }[/math] constructed from 2 binary sequences, X and Y. Z will also have length n and element values {+1,-1}. In principle, X and Y are restricted to be either symmetric or antisymmetric sequences. Z is derived by forming the inner product from the two seed sequences, X and Y, as follows:
The sequence, [math]\displaystyle{ Z=\left \{ z_i \right \} }[/math], may be balanced or unbalanced, as described above, or may be symmetric or antisymmetric. If, for example, the sequences X and Y are both symmetric so will also be Z. If both X and Y are antisymmetric, Z results to be a symmetric sequence. This is shown next:
In addition if one of X or Y is antisymmetric, and the other is symmetric, Z will be antisymmetric. In fact, the class of sequences X, Y which can form sequences Z with symmetric properties is wider than the class with seed sequences which are symmetric or antisymmetric.
As shown in [A.R. Pratt et al., 2006],[1] the circular crosscorrelation between two binary sequences, X and Y, of length n, is defined as:
where [math]\displaystyle{ k=\left ( i + r \right )mod n }[/math]. This operation corresponds to the formation of another type of derived sequence, [math]\displaystyle{ Z=\left \{ z_i \right \} }[/math], where the family members are determined through circular shifts of the original sequence members. In fact,
As we can see, the cross-correlation [math]\displaystyle{ R_{x,y}^c \left (r \right ) is then the balance, \lt math\gt \sum \left ( Z^r \right ) }[/math] of the sequence [math]\displaystyle{ Z^r }[/math].
In the following lines some examples of antisymmetric sequences are given for various lengths n. For length , it can be shown that there are two distinct antisymmetric sequences:
For , there are 3 distinct sequences, while for we can find 6. In the same manner, for we have 10 and for there are 20 such sequences. These were tabulated in MBOC Modulation with their cross-correlation values at zero offset.
References
- ^ a b c [A.R. Pratt et al., 2006] A.R. Pratt, J.I.R. Owen, G.W. Hein, J.-A. Avila-Rodriguez: Tracking Complex Modulation Waveforms- How to Avoid Receiver Bias, Proceedings of the International Technical Meeting of the Institute of Navigation, IEEE/ION PLANS 2006, 24-27 April, 2006, Loews Coronado Bay Resort, San Diego, California, USA.
Credits
The information presented in this NAVIPEDIA’s article is an extract of the PhD work performed by Dr. Jose Ángel Ávila Rodríguez in the FAF University of Munich as part of his Doctoral Thesis “On Generalized Signal Waveforms for Satellite Navigation” presented in June 2008, Munich (Germany)